La phylogénie est l’étude des relations de parenté entre les organismes. Les buts de la phylogénie sont, entre autres, d’étudier l’évolution des êtres vivants et d’estimer des temps de divergence depuis leur dernier ancêtre commun. Les étapes d’une analyse phylogénétique de données moléculaire consistent à obtenir les séquences des gènes (extraction génomique => PCR => séquençage), de les aligner, de calculer les distances ou les similarités entre les espèces (selon la méthode d’inférence choisie) et d’appliquer une méthode de reconstruction d’arbre. Une fois l’arbre phylogénétique obtenu, il faut pouvoir comparer les arbres puisque les différentes méthodes de reconstruction d’arbres donnent des résultats différents. De plus, selon les informations choisies pour effectuer l’analyse, les phylogénies diffèrent, car chaque gène possède sa propre histoire évolutive.

2. Comparaison d’arbres

Des métriques existent pour comparer objectivement les arbres. Les principales mesures de comparaison d’arbres sont les suivantes :

- Distance des moindres carrés (LS)

- Distance de Robinson et Foulds (RF)

- Distance des quartets (QD)

- Dissimilarité de bipartitions (DB)

Distance des moindres carrés (LS)

La distance des moindres carrés (Gauss, 1975) est la somme des différences entre la valeur observée et la valeur attendue au carrée. Il est souhaitable d’obtenir la valeur minimale. Son équation est illustrée ci-dessous :

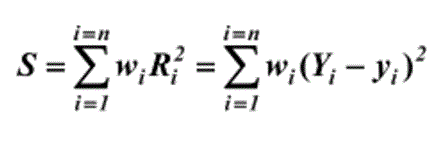
Où S = Somme

R = Résidu (différence entre la valeur observée et la valeur attendue)

(1) Équation de la distance des moindres carrés (Tirée de Wolberg, 2006)

Distance de Robinson et Foulds (RF)

La distance de Robinson et Foulds (Robinson et Foulds, 1981), aussi connu sous le nom de différence symétrique, est une mesure de distance topologique entre 2 arbres. C’est le nombre minimum d’opérations élémentaires ( $\alpha$ et $\alpha^{-1}$ , fusion et séparation de nœuds respectivement) pour passer d’un arbre T à un arbre T’ (Robinson et Foulds, 1981). La distance RF peut être également vue comme le nombre de bipartitions non partagées entre les 2 arbres (Felsenstein, 2004). Cette métrique prend la valeur 0 lorsque les deux arbres sont pareils. La figure 1 illustre un exemple de la distance de RF.

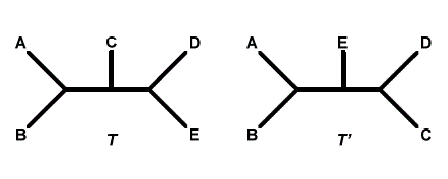
Fig 1. La distance RF entre les deux arbres T et T’ est d(T, T’)=2, soit la séparation du nœud entre D et E et la fusion de C et D. (Tirée de Tahiri, 2015)

Distance des quartets (QD)

La distance des quartets (Bryant et al., 2000) est le nombre de quadruplets (sous-arbre généré par 4 feuilles) qui ont une topologie différente dans les deux arbres considérés. La figure 2 illustre les différentes typologies que peut prendre un quadruplet.

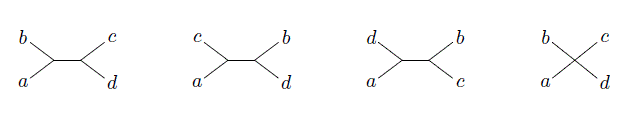
Fig 2. Les 4 topologies possibles du quadruplet formé par les espèces a, b, c et d (Tiré de Brodal et al., 2001).

Dissimilarité de bipartitions (DB)

La dissimilarité de bipartitions (Boc et al., 2010, Makarenkov et al., 2007) peut être considérée comme une mesure plus fine de la distance RF étant donné que cette dernière ne considère que les bipartitions identiques. Pour deux arbres ayant le même nombre de feuilles, on construit une table de bipartitions pour chaque arbre, chacune contenant les vecteurs de bipartition associés aux branches internes de l’arbre (0 pour les feuilles d’un côté et 1 pour les feuilles de l’autre côté) (Fig 3).

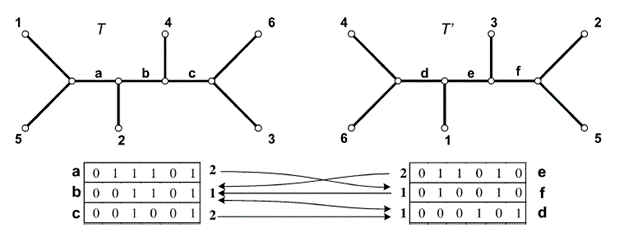
Fig 3. Deux arbres, T et T’, et leur table de bipartitions. Chaque ligne de la table de bipartition correspond à une branche interne. Les flèches indiquent les associations entre les vecteurs de bipartitions des 2 tables. Les valeurs en gras proches de chaque vecteur représentent la distance qui y est associé. (Traduit et tirée de Boc et al., 2010).

La distance bd est calculée comme suit :

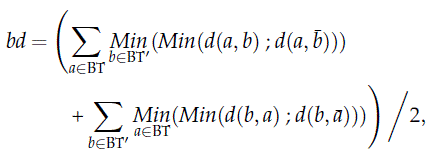
Où BT est la table de bipartitions de l’arbre T ;

BT’ est la table de bipartitions de l’arbre T’ ;

d(a, b) est la distance de Hamming entre le vecteur a et b ;

ā et ƀ sont les compléments des vecteurs a et b.

(2) Équation de la dissimilarité de bipartitions (Tirée de Boc et al., 2010)

Au-delà de la comparaison d’arbres, il faut également pouvoir retirer des informations des différents arbres obtenus. Plusieurs approches existent soit pour garder ce qui est commun aux arbres, les méthodes d’arbres consensus, soit pour fusionner les arbres en un seul, les méthodes de super-arbres. En effet, pour des projets tels que le Tree of Life (Madison, 2007), il est nécessaire de pouvoir fusionner des arbres ensemble et de retirer ce qui leur est commun.

II. Arbres de consensus

1. Méthodes principales

Les méthodes principales d’inférence d’arbres consensus sont les méthodes de consensus strict, de consensus majoritaire et de consensus majoritaire étendu (Fig 4). La méthode de consensus strict (Sokal et Rohlf, 1981) ne garde que les bipartitions présentes dans tous les arbres. Ainsi, seules les relations entre 2 taxons retrouvées dans tous les arbres sont conservées. La méthode du consensus majoritaire (Margush et McMorris, 1981) ne retient que les bipartitions présentes dans 50% (ou un autre pourcentage spécifié) des arbres. La méthode de consensus majoritaire étendu (Felsenstein, 1985), aussi connu sous le nom de « greedy consensus tree method », conserve les bipartitions de manière séquentielle. Les bipartitions sont ordonnées par ordre décroissant de fréquence d’occurrence. En suivant cet ordre, on choisit la bipartition la plus fréquente et on rajoute les autres bipartitions, une à une, selon leur compatibilité avec les bipartitions déjà choisies (Bryant et al., 2003).

Fig 4. Dans le cas d’un ensemble de 2 arbres, l’arbre de consensus strict est le même que l’arbre de consensus majoritaire (Tirée de Tahiri, 2015).

Les méthodes précédentes ont en commun qu’elles ne permettent d’obtenir qu’un seul arbre consensus. Ce n’est pas toujours idéal, car il y a souvent perte d’informations. Par exemple, dans la figure 5, l’approche classique d’arbre consensus majoritaire unique nous retourne une arborescence étoilée non informative alors que si on permettait des arbres consensus majoritaires multiples, on conserverait des informations potentiellement intéressantes.

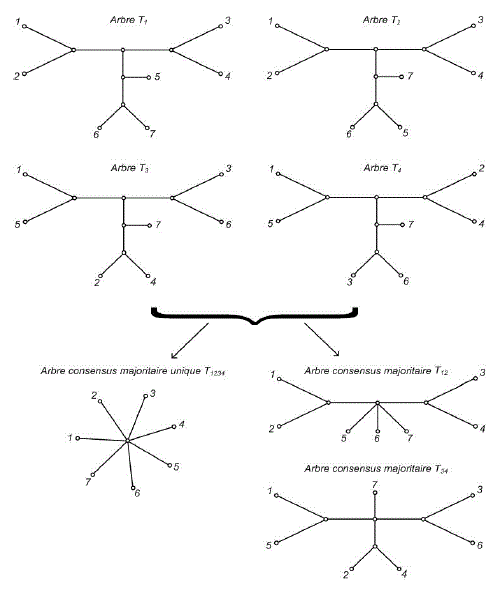
Fig 5. Quatre arbres phylogénétiques T1, T2, T3 et T4 définis sur un ensemble de sept feuilles ; leur arbre consensus majoritaire unique T1234; la solution à deux arbres consensus majoritaires T12 et T34 (Tirée de Tahiri et al., 2014).

L’étude de Tahiri et al. (2014 et présentement) propose un nouvel algorithme consensus-trees qui, à partir d’un ensemble d’arbres, permet d’obtenir un ou plusieurs arbres consensus en regroupant les arbres phylogénétiques.

2. Algorithme consensus-trees

L’algorithme consensus-trees est basé sur l’idée que classifier les arbres phylogénétiques avec l’algorithme des k-moyennes permettrait de séparer les familles de gènes avec la même histoire évolutive. Cet algorithme est basé sur l’algorithme des k-moyennes afin d’obtenir des partitions optimaux d’arbres. La distance de Robinson et Foulds a été utilisée et les critères d’évaluation CH (Calinski-Harabasz, 1974) et W (nouvelle fonction objective développée). La propriété utilisée est que selon la distance de Robinson et Foulds, l’arbre médian au sein d’un groupe d’arbres est l’arbre consensus (Barthélemy et McMorris, 1986).

Les données en entrée prises par l’algorithme sont n arbres phylogénétiques définis sur un même ensemble d’espèces (taxons). Tous les arbres doivent donc avoir les mêmes feuilles. Les données en sortie sont (1) le partitionnement optimal de l’ensemble d’arbres en un ou plusieurs groupes et (2) pour chaque groupe, (a) la liste des arbres qui s’y retrouvent; (b) l’arbre consensus du groupe; (c) la valeur des indices de CH et W.

Algorithme des k-moyennes

L’algorithme des k-moyennes partitionne de manière optimale un ensemble de données en k groupes selon un critère de similarité (MacQueen, 1968). Les étapes de l’algorithme standard sont les suivantes : (1) un nombre k de « moyennes » sont choisies aléatoirement parmi les éléments (i.e. : les données); (2) des groupes sont créés en associant chaque élément à la « moyenne » la plus proche selon une distance choisie; (3) le centroïde de chaque groupe est calculé et il devient la nouvelle « moyenne »; (4) les étapes 2 et 3 sont répétées jusqu’il y a convergence. Déterminer le nombre k de groupes optimal est souvent difficile. L’évaluation du k peut se faire après l’analyse avec un critère d’évaluation.

Propriété

Cette propriété a été décrite par Barthelemy et McMorris (1986). L’arbre médian d’un regroupement d’arbres est celui dont la distance totale avec tous les autres arbres de ce groupe est la plus petite possible. Dans le cas où cette distance est la distance RF, cet arbre médian correspond à l’arbre de consensus majoritaire lorsqu’il y a un nombre impair d’arbres dans ce groupe. Lorsque le nombre d’arbres dans le groupe est pair, il est possible d’avoir 2 arbres « médians » (Felsenstein, 2004).

La variante heuristique de l’algorithme des k-moyennes sur lequel est basé l’algorithme consensus-tree est celle implémentée par Makarenkov et Legendre (2001). La métrique choisie est la distance de Robinson et Foulds et les critères d’évaluation pour déterminer le k optimal sont CH et W.

Indice de CH

L’indice de Calinski-Harabasz (1974) permet de déterminer le nombre de groupe optimal pour, entre autres, l’algorithme des k-moyennes. Plus la valeur de l’indice est élevée, meilleur est le partitionnement des groupes. L’équation de l’indice CH est donnée ci-dessous :

(3) Équation de Calinkski-Harabasz (Tiré de Tahiri, 2015)

(4) Équation de l’indice d’évaluation intergroupe (Tirée de Tahiri, 2015)

(5) Équation de l’indice d’évaluation intragroupe (Tirée de Tahiri, 2015)

La limite de l’indice de CH est qu’il ne permet pas de déterminer le cas où k=1 (un seul groupe=> arbre consensus unique). Il n’est donc pas possible de comparer la situation de k=1 et les situations de k>2 à k=n-1 (plusieurs groupes dont au moins un groupe contenant ≥ 2 éléments => arbres consensus multiples).

Indice W (fonction objective)

(6) Équation de la fonction objective W (Tirée de Tahiri, 2015)

La nouvelle fonction objective W, dont l’équation se retrouve ci-haut, permet de calculer le cas d’un arbre consensus unique (k=1), mais il y a une perte d’informations concernant les distances intergroupes, puisque cette fonction ne prend en compte que la distance intragroupe.

Validation de l’approche et des critères

Des simulations seront effectuées afin de valider l’approche et le choix des critères. Le plan des simulations comprend 3 étapes :

(1) Générer k arbres phylogénétiques binaires aléatoires à n feuilles avec le site T-Rex (Boc et al., 2012) avec des paramètres de k={1…10} et n= {9,16,32,64).

(2) Générer pour chaque arbre T_i(où i=1…k),un ensemble de 100 arbres aléatoires appartenant à la classe i et ce, pour chaque intervalle suivant :

Intervalle I (0 à 10% de similitude);

Intervalle II (10 à 25% de similitude);

Intervalle III (25 à 50% de similitude);

Intervalle IV (50 à 75% de similitude);

Les pourcentages de similitude sont mesurés avec la distance RF.

(3) Appliquer l’algorithme consensus-trees aux ensembles d’arbres générés avec les différents paramètres (k, n, Intervalle, Fonction Objective W et le critère CH).

Résultats de l’étude préliminaire

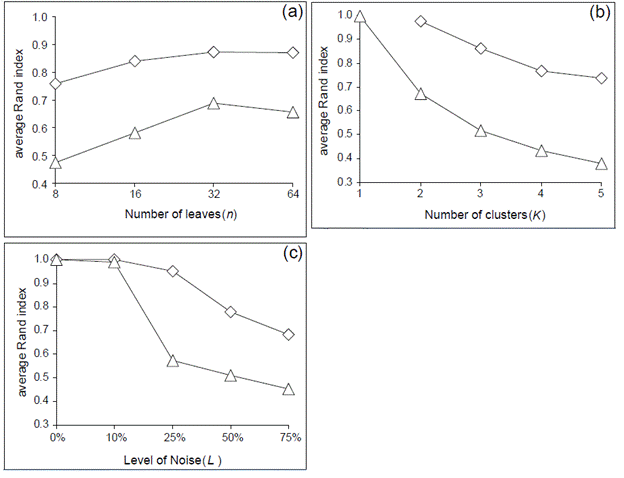
Fig 6. Étude préliminaire de l’évolution de l’indice Rand moyen (a) en fonction du nombre de feuilles (n); (b) en fonction du nombre de partitions (k); (c) en fonction du pourcentage de similitudes (L) entre les arbres phylogénétiques (Intervalle) pour les deux critères :

◊ Calinski-Harabasz; ∆ W (Tiré de Tahiri, 2015).

Pour les simulations, on connaît k, le nombre de groupes susceptibles d’être retrouvé par l’algorithme des k-moyennes. On sait également que les arbres appartenant aux intervalles plus bas (e.g. intervalle I) sont les arbres les plus éloignées. Pour connaître la force de l’algorithme, il faut donc regarder si les arbres éloignés sont regroupés ensemble ou non. L’indice de Rand est critère de fiabilité des groupes. Les résultats de l’étude préliminaire suggèrent qu’il est plus difficile de partitionner les arbres lorsque le nombre n de feuilles est élevé (Fig 6a). De même, plus il y a de groupes k, moins ils sont mis ensemble (Fig 6b). Plus les arbres sont éloignées (0 à 10%), plus il est difficile de bien les partitionner (Fig 6c).

En somme, l’algorithme consensus-trees est une méthode de partitionnement d’arbres phylogénétiques qui permet d’inférer des arbres consensus unique ou multiples selon le partitionnement obtenu. Il peut être appliqué autant pour la méthode de consensus strict, que les méthodes de consensus majoritaire ou consensus majoritaire étendu (Tahiri et al., 2014).

III. Super-arbre

1. Méthodes principales

La méthode des super-arbres permet de fusionner des arbres phylogénétiques d’espèces différentes (arbres sources) en un seul grand arbre contenant toutes ces espèces et le plus cohérent avec les arbres sources. Il faut par contre qu’il y a un chevauchement entre les feuilles des arbres sources. Cette méthode est particulièrement intéressante pour les jeux de données énormes; les analyses peuvent être faites sur des sous-ensembles de données et mises en commun par après. Plusieurs méthodes d’inférence de super-arbres existent dont la méthode de Gordon (1986) utilisé dans le passé, mais menant parfois à des incohérences. Présentement, une des méthodes les plus populaires est le MRP (Ragan, 1992; Doyle, 1992; Baum, 1992). La méthode du MRP (Fig 7) consiste à construire une matrice avec les arbres sources (1 pour les espèces partageant un nœud commun dans les arbres; 0 pour les autres espèces et ? pour les espèces non présentes) pour ensuite reconstruire l’arbre le plus parcimonieux (Von Haeseler, 2012).

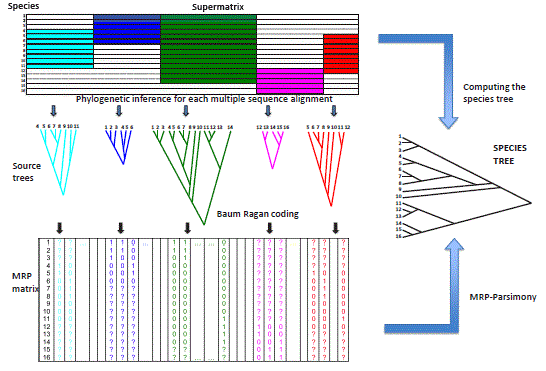
Fig 7. Étapes de la méthode MRP et de la méthode de supermatrice. La méthode MRP encode les données des arbres sources dans une matrice MRP avant d’appliquer une reconstruction de parcimonie pour obtenir le super-arbre d’espèces. La méthode de supermatrice prend la supermatrice de gènes concatenés pour obtenir l’arbre d’espèces (Tirée de Von Haeseler, 2012).

Les problèmes soulevés par les super-arbres sont similaires à ceux des arbres consensus : la nécessité de fusionner des arbres phylogénétiques pour des projets tels que le Tree of Life, l’incohérence de fusionner des arbres phylogénétiques et la perte d’informations et la perte d’informations et le mauvais recoupement des feuilles.

2. Algorithme Super-trees

L’algorithme super-arbre est une généralisation de l’algorithme précédent : au lieu de s’appliquer sur des arbres ayant les mêmes feuilles, il s’applique sur des arbres phylogénétiques partageant partiellement les mêmes feuilles. L’algorithme est également basé sur l’algorithme des k-moyennes.

Les données en entrées prise par l’algorithme sont n arbres phylogénétiques définis sur des ensembles d’espèces (taxons) différents, mais chevauchants. La particularité est qu’il faut filtrer les ensembles d’espèces et la difficulté réside en la détermination d’un seuil minimum de feuilles chevauchantes entre les arbres. Les données en sortie sont (1) le partitionnement optimal de l’ensemble d’arbres en un ou plusieurs groupes et (2) pour chaque groupe, (a) la liste des arbres qui s’y retrouvent; (b) le super-arbre du groupe; (c) la valeur des indices de W’ et W’’.

Fonctions objectives W’ et W’’

Les fonctions objectives W’ et W’’ sont utilisés comme indices dans l’algorithme Super-trees. Les équations de W’ et W’’ sont les suivantes :

(7) Équation de la fonction objective W’ (Tiré de Tahiri, 2015)

La fonction W’ est une variante de la fonction objective W. Pour chaque cas, il faut inférer le centroïde (super-arbre majoritaire), qu’il soit réel ou virtuel, ce qui devient coûteux.

(8) Équation de la fonction objective W’’ (Tiré de Tahiri, 2015)

La fonction W’’ est une autre variante de la fonction objective W, mais pour lequel il n’est pas nécessaire de calculer le centroïde à chaque cas.

Validation de l’approche et des critères

Le plan des simulations à venir comprend également 3 étapes :

(1) Générer k arbres phylogénétiques binaires aléatoires ayant n₁à n₂ feuilles dont au moins n feuilles communes avec le site T-Rex (Boc et al., 2012) avec des paramètres de k={1…10} et n= {9,16,32,64).

(2) Générer pour chaque arbre T_i(où i=1…k),un ensemble de 100 arbres aléatoires appartenant à la classe i et ce, pour chaque intervalle suivant :

Intervalle I (0 à 10% de similitude);

Intervalle II (10 à 25% de similitude);

Intervalle III (25 à 50% de similitude);

Intervalle IV (50 à 75% de similitude);

Les pourcentages de similitude sont mesurés avec la distance RF.

(3) Appliquer l’algorithme Super-trees aux ensembles d’arbres générés avec les différents paramètres (k, n, n₁, n₂, Intervalle, Fonction Objective= W’’ et les critères CH, BH, LogSS et Silhouette).

IV. Applications

L’algorithme Consensus-tree a été appliqué pour la classification des protéines ribosomales des archaebactéries. Le jeu de données de l’étude de Matte-Taillez et al. (2002) a été utilisé. Ces données consistent en 49 protéines ribosomales provenant de 14 archaebactéries. Les buts de l’application de l’algorithme Consensus-tree étaient de déterminer les protéines qui partagent la même histoire évolutive et la détection de gènes ayant subis les mêmes transferts horizontaux.

Les résultats de l’algorithme sont illustrés dans la figure 9. Le nombre de groupe optimal (k) déterminé par les critères CH et W sont k=2 et k=1 respectivement. Les 2 arbres consensus obtenus selon le critère de CH sont illustrés dans la figure 10 et l’arbre consensus obtenu selon le critère W, dans la figure 11. Le problème est qu’il y a présence de minimum local et de maximum local. Plusieurs scénarios de transfert horizontaux de gènes ont été également simulés selon les différentes valeurs de K, soit entre K=2 et K=5 (fig 11).

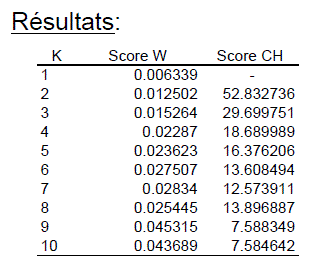
Fig 9. Résultats de l’algorithme Consensus-tree sur les données des protéines ribosomales des archaebactéries. Le k optimal pour le critère CH et W sont respectivement 2 et 1. (Tirée de Tahiri, 2015)

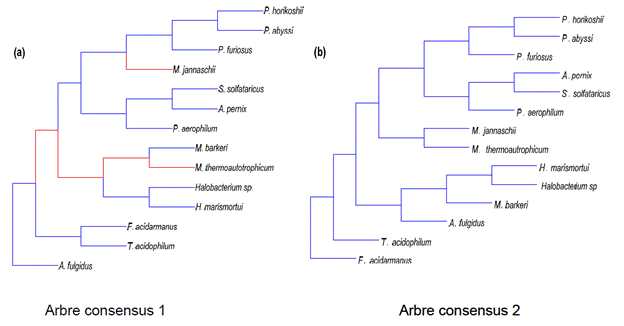
Fig 10. Arbres consensus obtenus selon le critère CH (Tirée de Tahiri, 2015)

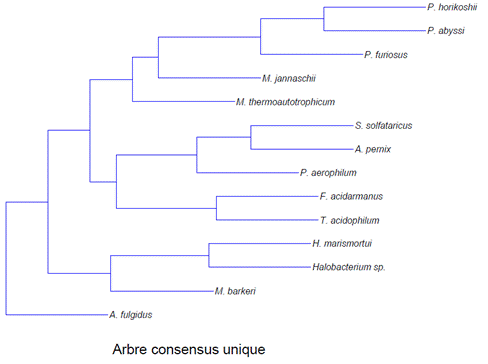
Fig 10. Arbre consensus unique obtenu selon le critère W (Tirée de Tahiri, 2015)

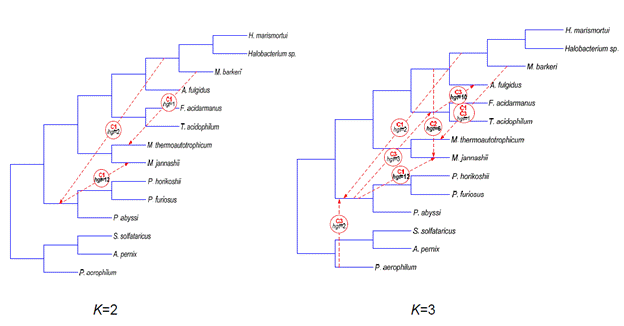
Fig 11. Scénario de transferts horizontaux selon le k. Ici, les cas k=2 et k-3 ont été illustrés. (Tirée de Tahiri, 2015).

Éventuellement, l’algorithme sera aussi appliqué à d’autres jeux de données tels que les papilionidés (Gepts et al., 2005), les marsupiaux (Cardillo et al., 2004), les mammifères placentaires (Beck et al., 2006) et les oiseaux de mer (Kennedy et Page, 2002).

Finalement, l’algorithme sera aussi appliqué pour étudier l’évolution des langues Indo-Européennes. La base de données provient de Dyen et al. (1997) et a été améliorée par Boc et al. (2010). Elle est regroupée en 200 mots de la liste Swadesh, traduite dans 87 langues et structurée en 1315 cognats. Le but de cette analyse est de trouver des groupes de langues partageant la même histoire évolutive et d’appuyer soit l’hypothèse Kourgane ou Anatolienne sur l’origine des langues indo-européenne ou peut-être émettre une nouvelle hypothèse.

En conclusion, les perspectives futures concernant les algorithmes proposés par Tahiri et al. (2014 et présent) sont d’appliquer davantage ces algorithmes à de vrais jeux de données et l’optimisation des algorithmes.

Références

Boc, A., Philippe, H., & Makarenkov, V. (2010). Inferring and validating horizontal gene transfer events using bipartition dissimilarity. Systematic biology, syp103.

Brodal, G. S., Fagerberg, R., & Pedersen, C. N. (2001). Computing the quartet distance between evolutionary trees in time O (n log2 n). In Algorithms and Computation (pp. 731-742). Springer Berlin Heidelberg.

Bryant, D. (2003). A classification of consensus methods for phylogenetics. DIMACS series in discrete mathematics and theoretical computer science, 61, 163-184.

Felsenstein, J., & Felenstein, J. (2004). Inferring phylogenies.

MacQueen, J. (1967, June). Some methods for classification and analysis of multivariate observations. In Proceedings of the fifth Berkeley symposium on mathematical statistics and probability (Vol. 1, No. 14, pp. 281-297).

Maddison, D. R., Schulz, K. S., & Maddison, W. P. (2007). The tree of life web project. Zootaxa, 1668 (Linnaeus Tercentenary: Progress in Invertebrate Taxonomy), 19-40.

Robinson, D., & Foulds, L. R. (1981). Comparison of phylogenetic trees. Mathematical Biosciences, 53(1), 131-147.

Tahiri, N., Willems, M. & Makarenkov, V. (2014). ) Classification d’arbres

phylogénétiques basée sur l’algorithme des k-moyennes, Proceedings of SFC 2014, Rabat, Morocco, 49-54.

Von Haeseler, A. (2012). Do we still need supertrees?. BMC biology, 10(1), 13.

Wolberg, J. (2006). Data analysis using the method of least squares: extracting the most information from experiments. Springer Science & Business Media.

Ce rapport a été créé suite à la conférence de Nadia Tahiri dans le cadre du cours BIF7002 : Séminaires en bio-informatiques le 17 février 2015 par Tissicca Hour et Chan David Puth.