INFÉRENCE PHYLOGÉNÉTIQUE BAYÉSIENNE ET MÉTHODE DE MONTE CARLO
Inférence phylogénétique bayésienne et méthode de Monte Carlo
1. Différentes méthodes d’inférence phylogénétique
La phylogénie moléculaire est l’étude de l’histoire évolutive
des espèces en utilisant une portion de leur séquence moléculaire qui aboutit au final à l’élaboration d’un arbre phylogénétique.
Un arbre phylogénétique est donc une forme de classification des espèces. Cette classification traduit les relations de
descendance des espèces avec modification de leurs caractère qui sont transmis d’une génération à l’autre à travers les
mécanismes d’hérédité. Lorsque l’on désire reconstruire un arbre phylogénétique, la première étape consiste à mettre en
correspondance les sites des séquences comparables que l’on obtient après alignement des séquences. Une fois les séquences
alignées, différentes méthodes de reconstruction d’arbres phylogénétiques peuvent être appliquées pour obtenir l’arbre qui
reflète le mieux les données. Nous vous présentons ci-dessous les différentes méthodes utilisées pour inférer ces arbres phylogénétiques :
1.1 Méthode basée sur les distances
L’approche basée sur les distances utilise une matrice
d’estimation de la distance évolutive appelée matrice de dissimilarités qui est obtenue en comparant les séquences deux à
deux. Elle a été introduite par Cavalli-Sforza23 et Edwards et Fitch et Margoliash24. Ces méthodes calculent une mesure de
distances (distances observées ou dissimilarités) entre toutes les paires d’espèces et construisent l’arbre avec des longueurs
de branches qui se rapprochent le mieux des distances (Figure 1).
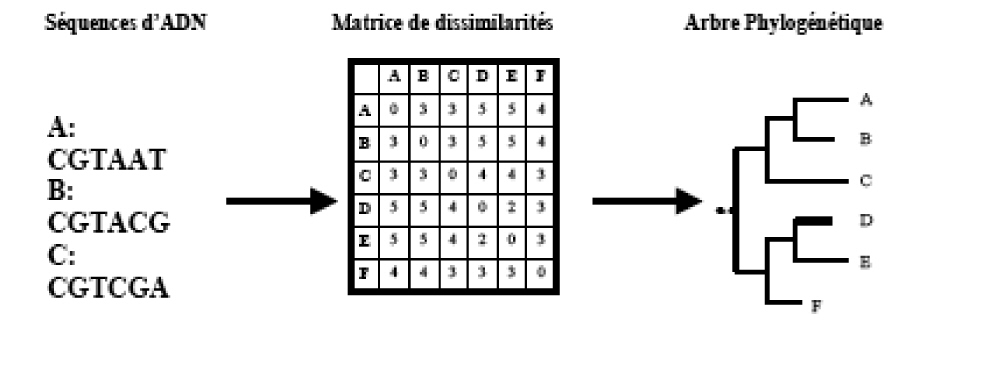
Figure 1 : Processus d’inférence phylogénétique par les méthodes de distances
Cependant, cette méthode fait appel à une distance observée
obtenue par une simple comparaison des séquences (non corrigée), ce qui entraîne deux biais majeurs :
1. la probabilité d’avoir plus d’une mutation à un site
donné augmente avec le temps de divergence entre deux séquences
2. la probabilité d’un changement dans un site peut être
différente selon les types de données.
Ces biais peuvent être corrigés par des méthodes faisant appel
à des modèles d’évolution. Après correction, il sera possible de mieux estimer la distance évolutive des séquences.
Les méthodes de distances utilisent donc une matrice de dissimilarités pour reconstituer la matrice de distances évolutives. Afin de
reconstituer la matrice de distances évolutives, différentes méthodes sont utilisées comme la méthode d’ajustement, celle de l'évolution
minimum et celle de regroupement.
1.1.1 Méthode d’ajustement
Le principe des méthodes d’ajustement est de choisir la
distance arborée la plus proche des données en utilisant un critère Q dont la forme générale est :
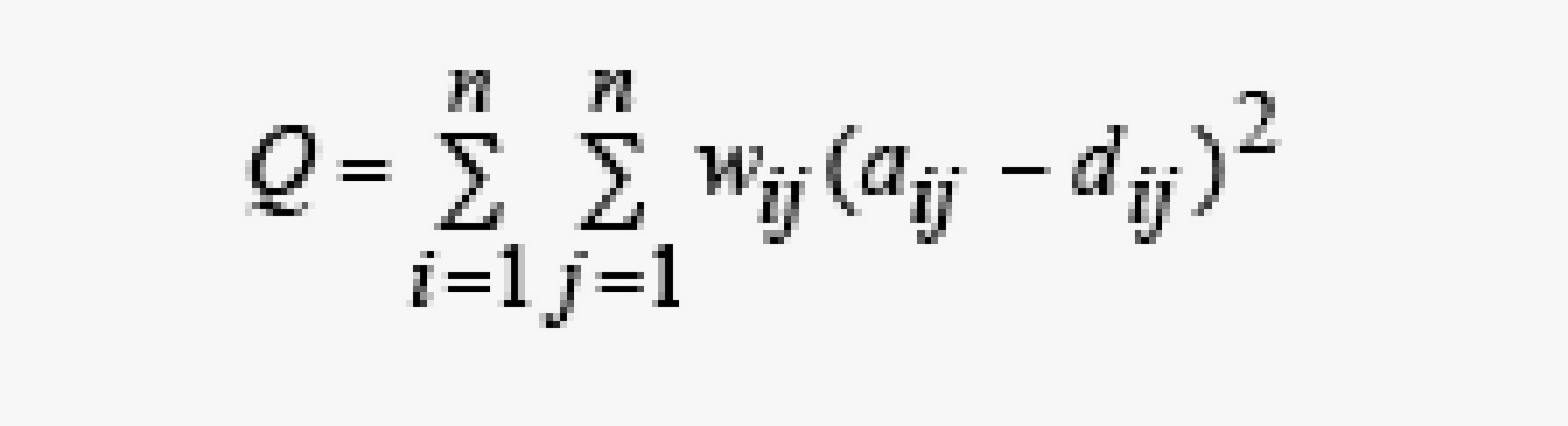
Une fois le critère choisi, la matrice de distance
arboré la plus proche est recherchée. Pour cela, il faut trouver une topologie d’arbre et des longueurs de branches qui minimisent le critère Q.
La base de cette méthode est NP-difficile. Cette méthode fait donc appel
à plusieurs heuristiques dont :
La recherche exhaustive: elle génère toutes les topologies possibles
d’arbres et ajuste les longueurs de toutes les arêtes selon les paramètres de la méthode. Cependant, cette méthode est limitée au traitement
de jeux de données restreints à 8 ou 9 espèces24.
principe issu de la programmation mathématique:cette méthode combine le critère
des moindres carrés avec un critère d’arborescence venant de la condition des 4 points. Ceci génère différentes matrices de dissimilarités provenant de
l’originale qui convergent vers une distance arborée25.
principe de la réduction:cette méthode utilise le critère des
moindres carrés et génère comme pour le principe issu de la programmation mathématique une suite de matrices de dissimilarités se rapprochant de la distance
arborée26. Cette méthode permet de traiter jusqu’à 50 espèces
1.1.2 Les méthodes de l'évolution minimum
Les méthodes d’évolution minimum se basent sur la longueur totale des branches de l’arbre
reconstruit. L’arbre est ajusté aux données et la longueur des branches est déterminée en utilisant la méthode des moindres carrés non pondérés. Les méthodes
d’évolution minimum requièrent un temps de calcul similaire à celui des méthodes d’ajustement. Le temps de recherche des topologies d’arbres peut également être
diminué en utilisant une recherche gloutonne27.
1.1.3 Les méthodes de regroupement (clustering)
Ces méthodes utilisent un algorithme sur la matrice de dissimilarités pour donner
directement un arbre. Elles sont très rapides, mais ne garantissent pas l’utilisation de toutes les distances28.
La méthode UPGMA (UnweightedPair-Group Method using Arithmetic Averages) peut être utilisée pour
inférer les phylogénies lorsqu’on suppose des taux d’évolution identiques sur toutes les lignées et qu’on considère le critère d’horloge moléculaire.
Contrairement à UPGMA, l’algorithme Neighbor Joining (NJ) n’assume pas l’horloge moléculaire
bien qu’il fonctionne mieux quand l’horloge est respectée29. La méthode autorise un taux d’évolution différent entre les lignées étudiées et utilise une
approche de regroupement combinée à une approximation efficace du principe d’évolution minimum. Elle permet d’inférer des phylogénies sur des centaines d’espèces
et elle garantit de retrouver la vraie phylogénie si la matrice de distance est une réflexion exacte de la phylogénie. Le principe de Neighbor Joining consiste
en la recherche séquentielle des voisins en minimisant la longueur totale de l’arbre (la somme des longueurs de branches) et en appliquant des procédures gloutonnes.
Pour reconstruire une phylogénie à partir d’une matrice de dissimilarités, cette matrice de dissimilarités est transformée pour obtenir un arbre en étoile (Figure 2).
Puis la paire de taxons qui minimise la longueur totale de l’arbre est choisie et remplacée par un noeud interne X. La dernière partie est reprise tant qu’il reste plus
de deux noeuds dans la matrice.
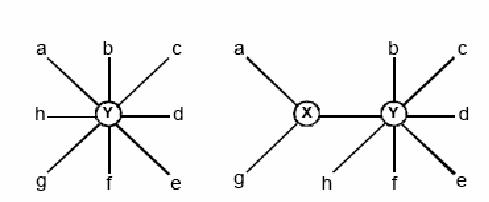
Figur 2. Expansion des nœuds par Neighbor Joining
1.2 Méthode basée sur les caractères
L’approche basée sur les caractères correspond à des méthodes plus robustes statistiquement
que les méthodes de distances mais elles sont plus lentes. Cette approche regroupe les méthodes de parcimonie, de maximum de vraisemblance et nouvellement
les méthodes bayésiennes (voir le point 2).
1.2.1 La parcimonie
La méthode de parcimonie consiste à rechercher parmi tous les arbres possibles et
toutes les séquences possibles de noeuds ancestraux, la combinaison qui minimise le nombre d’évènements mutationnels présents dans l’arbre reconstruit.
Elle s’appuie sur deux hypothèses principales30:
• Tous les sites évoluent indépendamment les uns des autres
• La vitesse d’évolution est lente et constante à travers les lignées évolutives.
Pour rechercher l’arbre le plus parcimonieux, plusieurs approches peuvent être utilisées.
Lorsque le nombre de taxons est inférieur à 10, il est possible d’effectuer une recherche exhaustive. Dans le cas contraire, il faut se contenter des constructions
heuristiques d’un arbre parcimonieux ou utiliser une approche de type branch-and-bound (séparation et évaluation).
Recherche exhaustive
La recherche exhaustive examine toutes les topologies possibles par une
approche gloutonne. Au début, elle regroupe trois espèces choisies arbitrairement ou selon des critères heuristiques. Puis elle ajoute une espèce sur la
branche conduisant à une longueur d’arbre minimale. Une autre espèce est ensuite ajoutée sur l’une des cinq branches possibles de l’arbre. Les itérations de
l’algorithme se terminent lorsque toutes les espèces ont été placées. Les algorithmes de Fitch (1971) et Sankoff (1975) sont parmi les plus connus pour cela.
Construction heuristique d’un arbre parcimonieux
Dans les constructions heuristiques d’un arbre parcimonieux, des algorithmes
itératifs s’ajoutent à la construction gloutonne de la recherche exhaustive. Ces algorithmes sont utilisés lorsque le nombre de taxons est supérieur à 20.
Les constructions heuristiques partent d’un arbre initial et essaient de trouver un arbre plus parcimonieux en effectuant des réarrangements de branches.
L’arbre initial est souvent inféré par des méthodes qui présentent une solution acceptable en un temps très court. Mais ces approches heuristiques ne couvrent
généralement que les topologies similaires à la topologie initiale. Par ailleurs, Il existe plusieurs stratégies de réarrangement ou de transformation de branches.
Les stratégies les plus connues sont31 :
• le réarrangement local (Nearest-Neighbor Interchanges "NNI");
• le réarrangement global (Subtree Pruning and Regrafting "SPR");
• la bissection et reconnexion d’arbres (Tree Bisection and Reconnection "TBR") ;
• les fusions d’arbres (tree-fusing) ;
• les algorithmes génétiques (Genetic algorithms).
La séparation et l’évaluation (branch-and-bound)
Un algorithme de séparation et évaluation a été proposé par Hendy et Penny en 198232.
Il permet de traiter une vingtaine de taxons en quelques minutes. Sa mise en place repose sur une propriété naturelle de la parcimonie : "la parcimonie
d’un sous arbre est toujours inférieure à la parcimonie de l’arbre tout entier". Comme pour les heuristiques de réarrangements, un arbre parcimonieux est
choisi au départ. Cet arbre et sa parcimonie (longueur d’arbre) P constituent l’arbre courant. Puis l’espace de tous les arbres possibles est exploré par
une procédure en profondeur. La racine de cet espace est un arbre à 3 feuilles. Les descendants d’un noeud-arbre sont issus de celui-ci par ajout d’une
nouvelle espèce à l’une de ses branches. La parcimonie de chaque noeud arbre est calculée. Tous les noeuds-arbres qui ont une parcimonie supérieure à P
ne sont pas étendus à cause de la violation de la propriété naturelle de parcimonie. Il y a un retour dans le parcours en profondeur pour effectuer un choix
alternatif. Ainsi si un arbre au complet est trouvé et sa parcimonie est égale à P, alors il est rajouté à la liste des arbres solutions. Si la parcimonie de
l’arbre complet est inférieure à P, cet arbre remplace tous les arbres solutions trouvés antérieurement et la parcimonie courante P est mise à jour.
La méthode de parcimonie est très sensible à l’ordre d’ajout des espèces. Elle donne souvent
plusieurs arbres solutions équivalents par la parcimonie mais de topologies différentes. Ces solutions sont souvent condensées dans un arbre consensus. Cet
arbre garde les noeuds les plus fréquents de l’espace de solutions. La parcimonie fournit le nombre de mutations de chaque branche. Mais elle n’effectue aucune
correction pour les substitutions multiples éventuelles sur les branches.
1.2.2 Le maximum de vraisemblance
Le maximum de vraisemblance a été introduit en phylogénie moléculaire par
Jerzy Neyman en 197133. Il évalue, en terme de probabilités (vraisemblance), l'ordre des branchements et la longueur des branches d'un
arbre dans le cadre d’un modèle d’évolution probabiliste donné.
La vraisemblance est la probabilité d'observer les données, soit les alignement
de séquences, en connaissant un arbre phylogénétique hypothétique. Deux hypothèses principales sont émises lors de l’utilisation de cette méthode:
• selon l’arbre donné, l’évolution est indépendante sur les différents sites
• l’évolution est indépendante selon les lignées.
La vraisemblance est calculée selon la formule:
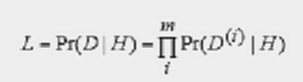
D(i) représente les données au site i.
H est l’hypothèse évolutive.
Le maximum de vraisemblance repose sur le calcul indépendant de la vraisemblance sur chaque site.
Il recherche la vraisemblance des données sous différentes hypothèses évolutives d’un modèle d’évolution et en retient les hypothèses qui rendent cette vraisemblance
maximale. Le maximum de vraisemblance cherche donc à trouver l'arbre dont la vraisemblance est maximale pour les séquences observées et le modèle d'évolution choisi.
Pour trouver l’arbre le plus vraisemblable, les bases de toutes les séquences à chaque site sont considérées séparément et le logarithme de la vraisemblance est calculé
pour une topologie donnée, en utilisant un modèle d’évolution particulier. Le logarithme de la vraisemblance est cumulé sur tous les sites et sa somme est maximisée
pour estimer la longueur des branches de l'arbre. Cette procédure est répétée pour toutes les topologies possibles et la topologie ayant la plus grande vraisemblance
est choisie.
Le maximum de vraisemblance est considéré comme plus fiable que les méthodes de distances et de
parcimonie. C’est la méthode qui conduit au résultat le plus proche de l'arbre évolutif réel en théorie. Comparé à la parcimonie, il est beaucoup plus robuste.
Il permet également d'appliquer les différents modèles d'évolution et d'estimer la longueur des branches en fonction du changement évolutif.
Par contre, c'est la méthode qui demande le plus de temps de calcul.
2. Les méthodes Bayésiennes
Les méthodes bayésiennes sont similaires au maximum de vraisemblance. Elles diffèrent
seulement par l’utilisation d’une distribution à priori de la quantité qui est en train d’être inférée. Elles sont plus rapides et permettent de traiter plus de taxons34.
Le théorème de Bayes
La notion de probabilité postérieure considérée ici est la probabilité de l’hypothèse H sachant les
données X : Pr (H | X), ce qui diffère du maximum de vraisemblance où l’on cherche la probabilité d’observer les données D sous une hypothèse X : Pr (D | X).
La probabilité postérieure d’une hypothèse pouvant être calculée par le théorème de Bayes, elle apparaît être fonction de la vraisemblance et de la probabilité a
priori de cette hypothèse :
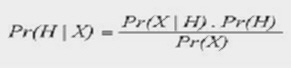
Pr (X | H) est la fonction de vraisemblance
Pr (H) est la probabilité a priori de l’hypothèse H
Pr (X) est la probabilité des données
La probabilité postérieure d’une hypothèse peut-être interprétée comme la probabilité que cette hypothèse soit vraie sachant les données
L’inférence bayésienne de la phylogénie
L’inférence bayésienne de la phylogénie combine la probabilité a priori Pr (T) d’un arbre
T avec la vraisemblance Pr (X | T) des données X sachant cet arbre T pour produire une distribution de probabilité postérieure Pr (T | X) sur les arbres en
utilisant la formule de Bayes :
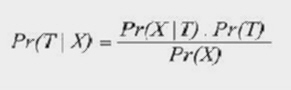
La probabilité postérieure d’un arbre pouvant être interprétée comme la probabilité que cet
arbre soit vrai sachant les données, les inférences sont réalisées à partir de la distribution de probabilité postérieure des différents arbres évalués au
cours de l’analyse. De manière analogue à la méthode du maximum de vraisemblance, l’arbre de probabilité postérieure maximale peut ainsi être déterminé facilement.
Mais l’approche bayésienne comporte certain problèmes comme la nécessité d’avoir une
distribution à priori sur les hypothèses. Ceci pose un problème si nous n’en avons aucune ou si elle est controversée. La méthode bayésienne est donc
souvent aoosicée à un model MCMC (Monte Carlo Markov Chain). L’idée sous-jacente aux MCMC est qu’une chaîne de Markov, prenant la forme d’une marche guidée à
travers l’espace multidimensionnel des paramètres, peut être utilisée pour estimer une distribution de probabilité en échantillonnant les valeurs de ces paramètres
de façon périodique. L’approximation de la distribution sera d’autant plus exacte que le nombre de pas effectués par la chaîne de Markov sera élevé.
3. Modèles d’évolutions utilisés pour les séquences protéiques
3.1 Les matrices protéiques
Si un système basé uniquement sur l'identité donne une sensibilité satisfaisante pour les
acides nucléiques, celui-ci devient moins approprié pour les séquences protéiques. Si l'on considère qu'un acide aminé peut être substitué à un autre en
fonction de certaines propriétés sans que la structure ou la fonctionnalité d'une protéine soit grandement altérée, on peut classer les acides aminés en familles
et obtenir ainsi un système de scores qui rende compte de l'affinité des résidus protéiques entre eux. Les matrices de scores qui en découlent permettront d'augmenter
la fiabilité des recherches de similitudes protéiques. Une des premières matrices à utiliser ce principe a été celle déduite de la dégénérescence du code génétique 35
Les scores élémentaires ont été alors déterminés en fonction du nombre commun de nucléotides présents dans les codons des acides aminés, ce qui revient à considérer
le minimum de changements nécessaires en bases pour convertir un acide aminé en un autre. Depuis de nombreuses matrices ont été créées et l'on peut classer celles-ci
en deux catégories. La première est celle qui regroupe plutôt les matrices issues d'études montrant le caractère de substitution des acides aminés au cours de
l'évolution et la deuxième est basée plus particulièrement sur les caractéristiques physico-chimiques des acides aminés. Nous présenterons ici les matrices les
plus couramment utilisées sans donner de liste exhaustive de toutes celles qui ont été déterminées.
3.2 Les matrices protéiques liées à l'évolution
3.2.1 Les matrices de type PAM, la matrice de mutation de Dayhoff
Elles sont sans aucun doute celles qui ont été les plus utilisées dans les programmes de comparaison de
séquences protéiques. Elles représentent les échanges possibles ou acceptables d'un acide aminé par un autre lors de l'évolution des protéines36. Elles ont été
déduites de l'étude de 71 familles de protéines (de l'ordre de 1300 séquences) très semblables (moins de 15% de différence) que l'on pouvait facilement aligner.
De ces alignements, une matrice de probabilité a été calculée où chaque élément de la matrice donne la probabilité qu'un acide aminé A soit remplacé par un acide
aminé B durant une étape d'évolution. Dayhoff utilisa une méthode basée sur la parcimonie pour générer la PAM. Les arbres phylogénétiques ont été estimés pour
différentes familles de protéines ainsi que les séquences ancestrales de ces arbres en utilisant une méthode de maximum de parcimonie. À partir de cela, les
informations ont été utilisées pour estimer les taux relatifs de remplacement d’acides aminés. Cette matrice de probabilité de mutation correspond en fait à une
substitution acceptée pour 100 sites durant un temps d'évolution particulier, c’est-à-dire une substitution qui ne perturbe pas l'activité de la protéine. On parle
ainsi d'une PAM (Percent Accepted Mutations) matrice. Si l'on multiplie la matrice par elle-même un certain nombre de fois, on obtient une matrice XPAM qui donne des
probabilités de substitution pour des distances d'évolution plus grande. Pour être plus facilement utilisable dans les programmes de comparaison de séquences,
chaque matrice XPAM est transformée en une matrice de similitudes PAM-X que l'on appelle matrice de mutation de Dayhoff. Cette transformation est effectuée en
considérant les fréquences relatives de mutation des acides aminés et en prenant le logarithme de chaque élément de la matrice. Des études de simulation ont montré
que la PAM-250 semble optimale pour distinguer des protéines apparentées de celles possédant des similarités dues au hasard. C'est pourquoi, la matrice PAM-250 est
devenue la matrice de mutation standard de Dayhoff. Cette matrice est basée sur un échantillon assez large et représente assez bien les probabilités de substitution
d'un acide aminé en un autre suivant que cette mutation engendre ou pas des changements dans la structure ou la fonctionnalité des protéines. Néanmoins, elle présente
un certain nombre d'inconvénients. Principalement, elle considère que les points de mutation, c'est-à-dire les positions d'échange des acides aminés sont équiprobables
au sein d'une même protéine37. Or, on sait que ceci n'est pas vrai et qu'une protéine peut présenter plusieurs niveaux de variabilité. De plus, l'ensemble des
protéines utilisées en 1978 n'est pas entièrement représentatif des différentes classes de protéines connues. Ainsi l'échantillon de 1978 était composé essentiellement
de petites molécules solubles très différentes des protéines membranaires ou virales que l'on peut étudier aujourd'hui. Ce constat a conduit à une réactualisation de
la matrice JTT (voir le point 3.2.4)38 en considérant 16 130 séquences issues de la version 15 de Swissprot, ce qui correspond à 2 621 familles de protéines. Cette
étude a permis de prendre davantage en compte les substitutions qui étaient mal représentées en 1978.?
3.2.2 Les matrices de type BLOSUM (BLOcks SUbstitution Matrix)
Une approche différente a été réalisée pour mettre en évidence le caractère de substitution des acides
aminés. Alors que les matrices de type PAM dérivent d'alignements globaux (cf. la recherche d'alignements optimaux) de protéines très semblables, ici le degré de
substitution des acides aminés a été mesuré en observant des blocs d'acides aminés issus de protéines plus éloignées. Chaque bloc est obtenu par l'alignement
multiple sans insertion-délétion de courtes régions très conservées (cf. la base BLOCK). Ces blocs sont utilisés pour regrouper tous les segments de séquences
ayant un pourcentage d'identité minimum au sein de leur bloc. On en déduit des fréquences de substitution pour chaque paire d'acides aminés et l'on calcule
ensuite une matrice logarithmique de probabilité dénommée BLOSUM (BLOcks SUbstitution Matrix). A chaque pourcentage d'identité correspond une matrice particulière.
Ainsi la matrice BLOSUM60 est obtenue en utilisant un seuil d'identité de 60%. Henikoff et Henikoff39, ont réalisé un tel traitement à partir d'une base contenant
plus de 2000 blocs.
3.2.3 Les matrices protéiques liées aux caractéristiques physico-chimiques
Les matrices liées à l'évolution regroupent assez clairement les propriétés chimiques et structurales
des acides aminés. Néanmoins, dans certains cas, elles ne suffisent pas toujours pour révéler au mieux certaines caractéristiques physico-chimiques communes à
deux protéines. C'est pourquoi des matrices basées essentiellement sur ces propriétés ont été déterminées. Les plus courantes sont celles basées sur le caractère
hydrophile ou hydrophobe des protéines et sur leur structure secondaire ou tertiaire. On peut citer parmi celles-ci, la matrice d'hydrophobicité basée sur des mesures
d'énergie libre de transfert de l'eau à l'éthanol des acides aminés40 ou la matrice de structure secondaire basée sur la propension d'un acide aminé à être dans une
conformation donnée41. Plus récemment l'augmentation du nombre de structures tridimensionnelles déterminées, a permis d'établir des matrices basées sur la comparaison
de ces structures. Ces matrices peuvent être utilisées pour comparer des protéines relativement éloignées. Parmi celles- ci, nous pouvons citer la matrice établie par
Risler et al.42 obtenue par la superposition des structures 3-D de 32 protéines réunies en 11 groupes de séquences très voisines et la matrice de Johnson et
Overington43 développée à partir de l'étude de 235 structures protéiques regroupées en 65 familles de protéines pour lesquelles on connaissait au moins la structure
tridimensionnelle de trois séquences.
3.2.4 Le modèle JTT
Jones, Taylor, and Thornton (1992) ont développé une procédure plus rapide et automatisée basée sur
le modèle de Dayhoff pour réaliser leurs matrices JTT. Ils ont utilisé l’approche de Dayhoff pour produire leur matrice à partir d’une base de donnée plus large.
Après avoir estimé l’arbre phylogénétique pour chaque famille de protéine de la base de donnée, leur méthode sélectionne une paire de séquences les plus voisines
avec 85% d’identité et leurs différences sont comptées. Les deux paires analysées sont ensuite éliminées et le processus répétés pour toutes les paires de séquences
de toutes les différentes familles de protéines.
3.2.5 Le modèle WAG
La majorité des méthodes de vraisemblance pour construire des arbres phylogénétiques à partir d’acides
aminés sont basées sur des models empiriques d’évolution des protéines. Ces modèles ont besoin de bonnes matrices de remplacement afin d’estimer de façon précise les
distances d’évolution véritables et les relations entre les espèces. Cependant aucune des matrices utilisant le maximum de parcimonie est entièrement satisfaisante.
Le maximum de parcimonie assume que pour chaque site donné d’un alignement, seulement un seul changement a eu lieu par site pour construire l’arbre. Ceci conduit à
une sérieuse sous-estimation du vrai nombre de changements qui ont eu lieu, ce qui pourrait conduire à des erreures systématiques. Le modèle de Dayhoff est très
affecté par ce problème. La règle des 85% du modèle JTT réduit ce problème mais ne le résolu pas car toutes les informations qui sont offertes par les séquences
avec moins de 85% d’identité ne sont pas considérées. Whelan et Goldman44 ont combiné les meilleurs attributs de la vraisemblance et des méthodes de comptage
pour estimer un modèle de remplacement d’acides aminés à partir d’une large base de donnée de différentes familles de protéines globulaires (3905 séquences d’acides
aminés réparties en 182 familles de protéines) en utilisant une approximation basée sur le maximum de vraisemblance. Ce modèle semble fournir une meilleure estimation
du processus d’évolution et peut être appliqué dans des études phylogénétiques plus larges concernant les séquences protéiques que les modèles estimés en utilisant des
approches de vraisemblance.
3.2.6 Le modèle de Poisson
Ce modèle assume une fréquence stationnaire et un taux de substitution homogènes entre les
acides aminés23. Il est l’équivalent du modèle Jukes-Cantor pour les séquences d’acides nucleiques.
3.2.7 Le modèle GTR
C’est le modèle le plus général. Il permet une flexibilité à la fois au niveau des fréquences
stationnaires et au niveau des taux de substitution entre les acides aminés. Il engendre donc ainsi plusieurs paramètres ; 19 paramètres de fréquence
stationnaire et 189 paramètres de taux de substitution.
4. Le modèle CAT
Les modèles standards de substitution assument que tous les sites d’un alignement de proteines sont
soumis aux mêmes processus de substitution. C’est à dire même taux relatif d’échange entre acide aminés ρ et même fréquence stationnaire π (i.e fréquence
relative de chacun des acides aminés à l’intérieur des proteines alignées). Or, Lartillot et Philippe (2004) suggèrent un modèle où la matrice de substitution (Q)
serait différente d’un site à l’autre. Nous parlons donc d’un modèle dit hétérogène où chaque site de l’alignement proteique appartient à une catégorie (ou classe)
regroupant d’autres sites partageant le même profil de fréquence stationnaire π et donc la même matrice de substitution puisque Qij = ρij x πj.
La Figure 3 représente l’idée générale du modèle CAT.
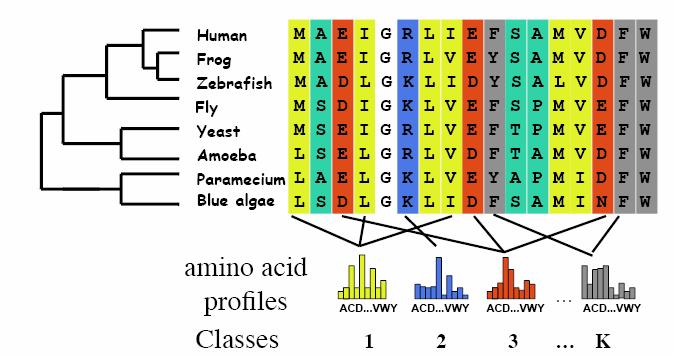
Figure 3 : Vue générale du modèle CAT
Le nombre total de classes (k) à priori ainsi que leur profil de fréquence stationnaire respectif
est déterminé par un mécanisme de Dirichlet22 tandis qu’un Gibbs Sampling22 est utilisé pour associer à chacun des sites, via la variable d’allocation ziε[1..N] Ε [1..k],
la classe repésentant le mieux sont profil d’acide aminé. N étant la longueur des séquences proteiques à l’intérieur de l’alignement. L’inférence d’un arbre phylogénétique
à partir d’un alignement de séquences sous le modèle CAT se fait par la méthode Bayésienne Markov Chain Monte Carlo (MCMC). L’algorithme génère à chaque cycle de nouvelles
valeurs pour les paramètre du modèle de façon à maximiser p(θ | D,M ) qui est la probabilité que l’arbre choisis ainsi que ces paramètres (θ) soit la meilleure représentation de la phylogenie
des espèces en question sachant l’alignement des leur proteines (D) et ce sous le modèle CAT (M). Parmis les paramètres (θ) qui sont mis à jour au fil des cycles, mentionnons la topology de
l’arbre (τ), la longueur des branches (t), la matrice des taux relatifs d’échange entre acides aminés (ρ), le nombre de catégories de site (k) ainsi que leur profil de fréquence stationnaire respectif Πc.
La figure 4 représente la courbe ROC illustrant la convergence vers un état maximale de p(θ | D,M).
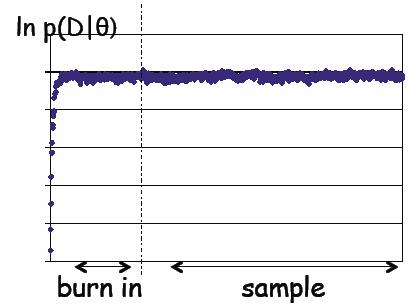
Figure 4 : Probabilités postérieures obtenue par MCMC
La phase Burn In correspond aux premiers arbres générés par la MCMC et sont exclus afin de ne pas
perturber la qualité de l’échantillonnage fait dans la phase suivante. C’est dans la phase d’échantillonage que différents θ sont choisis au hasard et sont utilisés
pour en déduire,par une moyenne des valeurs des paramètres, l’arbre représentant le mieux la phylogenie des séquences analysées.
Les phénomènes d’homoplasie (convergence et réversion), souvent dû aux saturations de sites
(multiple mutations à un même site au cours de l’évolution), engendrent souvent l’inférence d’arbres phylogénétiques erronés. Un exemple fréquemment rencontré
est celui de l’attraction des longues branches (LBA) où les espèces à évolution rapide ont tendance à être regroupés ensemble malgré qu’ils aient des évolutions
différentes . La figure 5 présente un exemple de phénomène d’homoplasie1.

Figure 5 :Exemple de convergence et de réversion
Notons le cas de convergence où deux états D convergent vers l’état E
sur deux branches éloignées de l’arbre réel. L’erreur que certains programmes d’inférence phylogénétiques auraient tendance à faire serait de rapprocher les espèces impliquées alors qu’en
réalité ils ont des histoires évolutives complètement différentes. Le cas de réversion est celui où l’état V subit une mutation vers l’état I pour ensuite
revenir à l’état initial V sur la dernière branche de l’évolution ( séquence 27). L’erreur serait ici de placer la séquence 26 loin de la séquence 27 dû à
leur divergence au niveau de la position j.
La figure 6 présente un exemple simplifié du phénomène LBA dû à la saturation des sites.
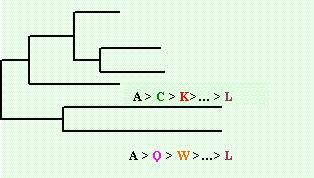
Figure 6 :Exemple de LBA
On remarque que les deux espèces ayant un taux d’évolution plus rapide que les autres partagent
le même ancêtre direct alors qu’ils ne devraient pas étant donné qu’ils ont deux chemins d’évolution différents.
Lartillot, Brinkmann et Philippe (2007) ont comparé les résultats d’inférence Bayésienne d’un
arbre phylogenetique à partir de séquences provenant de différents organismes du règne animal sous le modèle CAT et sous le modèle WAG (Whelan-Goldman). WAG
étant un modèle assumant que tous les sites sont soumis au même mécanisme d’évolution i.e. une seule matrice de substitution (Q) pour tous les sites.
Les figure 7 et 8 présentent les résultats obtenus sous WAG et CAT respectivement.

Figure 7 : Arbres consensus obtenus par inférences Bayesienne sous le modèle WAG :
Champignons (Bleu fonçé), Deuterostomes (Gris), Choanoflagellés (Bleu ciel,B et D),
Platyhelminthes (Orange, C et D) , Nématodes (Rouge, A et B),Arthropodes (Vert)

Figure 8 : Arbres consensus obtenus par inférences Bayesienne sous le modèle CAT :
Champignons (Bleu fonçé), Deuterostomes (Gris), Choanoflagellés (Bleu ciel, B et D),
Platyhelminthes (Orange, C et D) , Nématodes (Rouge, A et B),Arthropodes (Vert)
Sous WAG, on remarque en A et C que les Nématodes et les Platyhelminthes respectivement,
qui sont deux groupes à évolution rapides sont soumis aux LBA avec le Outgroup des Champignons. Ce qui a pour effet de rapprocher les Deuterostomes et
les Arthropodes et de créer un effet d’émergence basale respective des Nématodes et des Platyhelminthes. Cet effet de LBA est corrigé lorsque le groupe
de Choanoflagellées est ajouté au Outgroup. La longue branche séparant le Outgroup du Ingroup est ainsi racourcie et a pour effet de rapprocher ensemble
les Arthropodes et les Nématode (B) / Platyhelminthes (D) sous un même ancêtre commun direct.
Sous CAT, les auteurs ont obtenu de meilleurs résultats du fait qu’aucun des quatres arbres obtenus
ne comporte de LBA. CAT serait donc plus sensible à la détection de saturation des sites et d’homoplasie menant au phénomène de LBA grâce au caractère site hétérogène
du modèle
5. Le modèle CAT-BP
Blanquart et Lartillot (2008) proposent d’améliorer le modèle CAT en lui ajoutant une dimension
temporelle non-stationnaire; la portion ‘Non-Stationnary Break-Point (BP)’.Cette portion BP augmente la sensibilité du modèle au phénomène d’homoplasie en assumant
que l’hétérogénécité du processus de substitution ne se situe pas seulement aux niveau des sites proteiques mais aussi au niveau de l’espace temporel de l’évolution.
Ce modèle soutient le fait que les profils de fréquences stationnaires des acides aminés seraient modifiés au cours du temps et divergeraient entre les groupes d’espèces
à partir d’un certains Break-Point. La figure 9 illustre le modèle de substitution chimère hétérogène/ non-sationnaire CAT-BP.
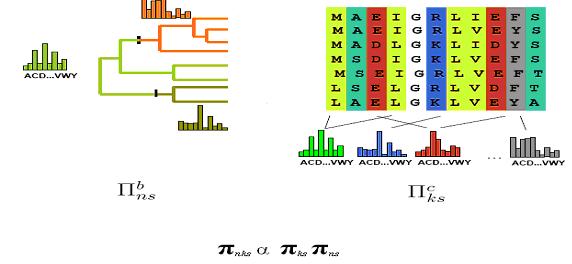
Figure 9 : Le modèle CAT-BP
Πb et Πc représentent respectivement l’ensemble des profils
de fréquences stationnaires des 20 acides aminés s pour les différents groupes phylogénétiques n délimités par les Break-Point et pour les différentes classes k de
sites de l’alignement proteiques. La fréquence stationnaire d’un acide aminé s du groupe n et de la classe k est donc
πks x πns
Les valeurs des paramètres de la portion BP (nombre de groupes phylogénétiques n, les profils d’états
sationnaires Πb, l’emplacement des Break-Point) du modèle CAT-BP, tout comme c’est le cas pour la portion CAT, sont établies à priori par un mécanisme de Dirichlet
et de Gibbs Sampling. Ces valeurs sont ensuite mises à jour lors de chaque cycles MCMC visant à maximiser la probabilité à post-priori p(θ | D, CAT-BP).
Les auteurs ont voulu prouver la supériorité de ce modèle CAT-BP par rapport à trois autres modèles soit
GTR (site- and time-homogeneous general time–reversible)4, CAT, et BP6. GTR étant un modèle assumant qu’il y a une seule matrice de substitution stationnaire
dans le temps et homogènes pour tous les sites de l’alignement. Pour ce faire ils ont utilisé leur méthode d’inférence Bayésienne pour inférer un arbre de proteines
mithochodriales de 20 espèces d’arthropode (Lartillot et Blanquart 2008). Les résultats obtenus pour chacun des modèles sont présentés à la figure 10.

Figure 10 : Inférence phylogénétique Bayésienne de vingt espèces d’artropodes sous
A) GTR B) BP C) CAT D) CAT-BP
Notons que les modèles GTR, BP et CAT infèrent une perte de monophylie des chelicerates et des insectes
en positionnant les abeilles Apis mellifera et Melipona bicolor parmis les chelicerates. Cet artefact réussi par contre à être évité avec le modèle CAT-PB.
Cette perte de monophylie des chelicerates et des insectes générée par GTR, BP et CAT serait dû en un premier temps au phénomène de LBA entrainant une saturation
des sites causé par l’évolution rapide de Apis, Melipona et de Varroa. Deuxièmement, l’artefact serait aussi étroitement lié au fait que ce sont ces trois espèces
qui ont la composition nucléotidique la plus rich en A-T; 81% pour Melipona, 79% pour Apis, et 75% pour Varroa. Un modèle tel CAT – BP, à l’affût des differents
profils de substitution possible autant au niveau de l’évolution des taxon qu’au niveau des sites proteiques, semble donc nécessaire pour détecter les phénomène de
saturation des sites et d’homoplasie pour ainsi empêcher l’inférence d’arbres phylogénétiques biaisés par les LBA.
6. Le modèle CAT – BP pour inférer la température optimale (OGT) de croissance du dernier ancêtre universel
commun (LUCA)
Au cours de l’évolution, l’effet de la température à laissé des empreintes (Footprinting) sur certaines
proteines et ARN ribosomale (ARNr) dont l’analyse est utile pour inférer l’OGT probable de LUCA et de ses descendants les bactéries, les archaebactéries et
les eucaryotes. A la figure 11 apparait une représentation simplifiée de l’arbre phylogénétique de la vie avec les trois grands groupes d’êtres vivants retrouvés
sur la terre descendant de l’ancêtre hypothétique LUCA.

Figure 11 : L’arbre phylogénétique de la vie
La stratégie habituellement utilisée pour inférer l’OGT des taxons ancestraux est de contruire un
arbre phylogénétique à partir d’alignement d’ARNr ou de proteines universelles de plusieurs espèces couvrant l’étendue de l’arbre de la vie et d’en évaluer
l’évolution du contenu en nucléotide G+C (pour l’ARNr) et en acides aminés IVYWREL (pour les proteines). Selon certaines études, le pourcentage élevé de ces
nucléotides et acides aminés à l’intérieur des macromolécules serait étroitement lié au caractère thermophile d’un organisme (Galtier et al. 1997,
Zeldovich et al. 2007).
Galtier et al. (1999) ont inféré un arbre à partir d’ARNr et en sont venu à la conclusion que LUCA
aurait été non-hyperthermophile. Par contre, Di Giulio et al. (2003) ont démontré le contraire à partir d’un alignement de proteines. Ces résultats
contradictoires laissent supposé l’innefficacité du modèle de Di Guilio basé sur une matrice de substitution stationnaire et homogène.
Lartillot et al. (2008) décident d’intervenir en utilisant leur modèle CAT-BP sur deux inférences parallèles.
L’une à partir de séquence d’ARNr double brin provenant de 456 organismes différents et l’autres à partir de proteines universelles de 30 organismes. Les deux types
d’analyses convergent vers les trois conclusions clées suivantes; 1) LUCA aurait été un organisme non-hyperthermophilique; supporté par Galtier et al. (1999)
2) L’ancêtre des bactéries et celui des archaebactéries auraient éventuellement évolué de thermophile à hyperthermophile; supporté par les traveaux de
Gaucher et al. (2003) ainsi que par ceux de Gribaldo et al. (2006) 3) A l’intérieur de l’arbre phylogénétique des bactéries, il y a diminution de la tolérance
aux hautes températures; en accord avec les études de reconstruction de la proteine procaryotique ancestrale EF-Tu qui aurait eu une température optimale située
entre 55oC et 65oC Gaucher et al. (2008). La figure 12 shématise l’évolution de la thermophilie basée sur les résultats d’inférence obtenus par Lartillot et al (2008).
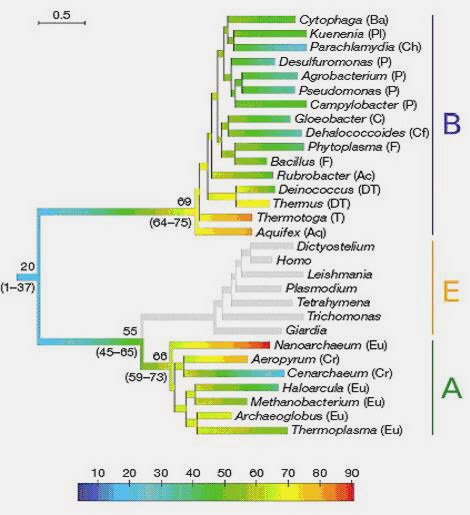
Figure 12 : Evolution hypothétique de la thermophilie : B Bactéries
E Eucaryotes A Archaebactéries
L’hypothèse comme de quoi LUCA aurait été un organisme non-hyperthermophile est appuyé par d’autres
études qui abordent dans le même sens. Par exemple, il a été avancé que le code génétique ancestral de LUCA ne pouvait pas coder pour les acides aminés IVYEW et
limitait ainsi ses proteines à opérer strictement sous des conditions de faible température (Fournier et al. 2007). Aussi, des modèles géologiques d’inférence de
climat archaique suggèrent qu’il y a 4.2 milliard d’années la terre aurait été plus froide qu’elle ne l’est aujourd’hui, possiblement recouverte d’océans glacés
(Nisbet et al. 2001). De plus, d’autres études suggèrent qu’il y aurait eu environ 2 milliards d’années plus tard l’impact d’une météorite avec la terre qui aurait
engendré une hausse brutale de la température des océans (Nisbet et al. 2001, Sleep et al. 1989,Gogarten et al. 1995) et donc éventuellement l’apparition des
organismes thermophiles comme le soutient le modèle de Lartillot et al.
Finalement, toujours pour appuyer l’hypothèse de Lartillot et al. et tenter d’expliquer comment
l’évolution aurait pu passer du mode mésophile au mode thermophile, il a été proposé que LUCA possédait un génome à ARN et donc peu résistant aux températures
élévées et que ses descendants auraient développé l’habilité d’utiliser l’ADN (Mushegian et al. 1996) probablement après avoir fait des copies de séquences
virales (Forterre et al. 2002). La figure 13 shématise les hypothèses géologiques et biologiques d’un monde ayant transitionné d’un état mésophile à thermophile.
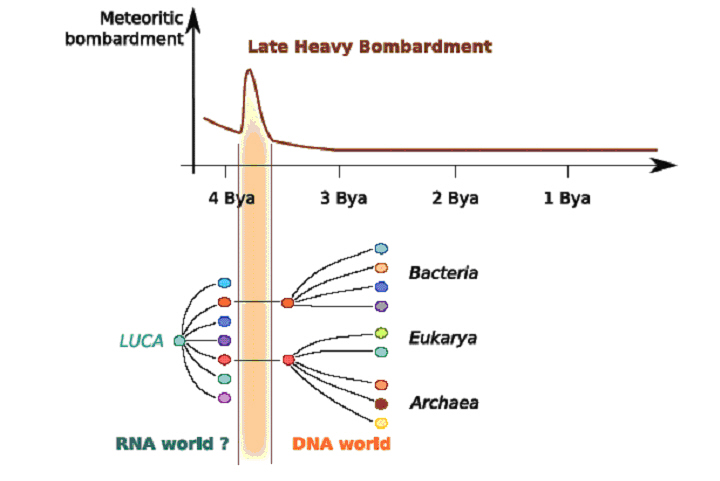
Figure 13 : Hypothèses expliquant la transition mésophile vers thermophile
7.Phylobayes versus MrBayes
Nous avons inféré l’arbre phylogénétique de trente espèces éloignées en utilisant le programme
Phylobayes v2.3 développé par le groupe de Lartillot et avons ensuite comparé les résultats obtenus avec
le programme MrBayes v3.1 Les deux prorammes utilisent une approche bayésienne jumelée à une procédure MCMC mais contrairement à MrBayes qui supposent que tout les sites de
l’alignement évoluent de façon homogène, Phylobayes utilisent le modèle CAT décrit ci-haut.
Nous avons utilisé comme données un alignement multilpe de séquences proteiques d’ARN polymérase1
(RNApol1) (599 acides aminés) fournit avec l’archive Phylobayes. L’alignement en format Nexus est présenté ici. Afin de mettre l’emphase sur les différences
associées uniquement à l’utilisation de CAT, nous avons procéder aux inférences en choisisant pour les deux programmes l’option Poisson comme modèle d’évolution.
Les deux programmes ont été utilisés en console sous une architecture Linux. Avec Phylobayes,
la mise en fonction de la MCMC nécessite l’exécution de la commandes suivantes;
./pb –d MSA.ali rnapol1
qui demande de lire le fichier MSA.ali contenant l’alignement multiple et d’enregistrer
les résultats dans différentes extension rnapol1.
Afin de nous renseigner sur la qualité de l’inférence nous avons démarré en parallèle une
seconde MCMC à l’aide de la commande suivante. De cette façon il est possible de vérifier la convergence de deux chaînes séparées.
./pb –d MSA.ali rnapol2
La commande à exécuter pour arrêter le programme est
./stoppb rnapol1 pour arrêter la première chaîne
./stoppb rnapol2 pour arrêter la deuxième chaîne
Le tutoriel mentionne qu’il est possible de vérifier la qualité des chaînes obtenues en mesurant
leur niveau de convergence à l’aide de la commande suivante;
./bpcomp –x 100 2 rnapol1 rnapol2
qui demande de rejeter les 100 premier arbres (burnin) de chaque chaîne et de procéder à une
comparaison à tous les deux arbres de chacune des chaînes. Cette commande génère un fichier dans lequel on y trouve une valeur de score maxdiff qui est un
indice de la qualité des MCMC. L’auteur suggère qu’idéalement le maxdiff devrait être inférieur à 0.1. Dans notre cas, nous avons laissé tourner l’algorithme
pendant 15 minutes et généré ainsi une MCMC de 10000 arbres. Plus le nombre de cycles de générations d’arbres est élevé meilleure est la qualité de l’inférence.
Puisque nous avons obtenu une valeur maxdiff de 1, nous en concluons que l’échantillon d’arbres générés n’a pas été suffisamment élevé pour en arriver à une
convergence des valeurs de vraissemblance (likelihood) à l’intérieur de la phase de burn out. La commande ./bpcomp génère aussi un ficher contenant l’arbre consensus
moyen généré par les deux chaînes.
L’arbre consensus que nous avons ainsi obtenu est présenté sous format Newick à l’intérieur du
fichier ArbrePB_2.txt Nous avons comparé cet arbre avec celui généré par les auteurs du programme (consensus obtenu sous un maxdiff < 0.1) (ref. ArbrePB_1.txt)
à l’aide d’un applet java de comparaison d’arbre phylogénétique46. Selon ce programme, les deux arbres sont similaires à 94.2%. Le résultat est présenté à la figure 14.
On peut y remarquer que les arbres respectent la phylogénie moyenne retrouvée dans la littérature et que la seule différence majeure entre les deux arbres est le
postionnement de Dicyostelid.
_PB(1).jpg)
Figure 14 : Comparaison d'inférence phylogénétique avec Phylobayes:
Phylobayes (2): maxdiff = 1
Phylobayes (1): maxdiff < 0.1
Pour obtenir l’arbre consensus généré par chaque chaîne séparément, il suffit d’entrer la
commande suivante (ici pour rnapol1)
./readpb –x 100 10 rnapol1
ou les valeurs 100 et 10 constituent les critères d’échantillonnage
Phylobayes offre aussi de comparer l’inférence sous CAT avec d’autres modèles d’évolution tels WAG et GTR et
d’obtenir des valeurs statistiques de qualité à l’aides des commandes cvrep, readcv et sumcv.
La suite de commande à exécuter avec MrBayes se résume ainsi
Lire le fichier Nexus contenant l’alignement;
./execute MSA.nex
Choisir le modèle d’évolution
./prset aamodelpr=fixed rates=invgamma
Démarrer la MCMC
./mcmc ngen=10000 samplefreq=10
Résumer l’échantillonage des paramètres inférés
./sump burnin=250
Résumer l’échantillonage des arbres inférés
./sumt burnin=250
Tout comme avec Phylobayes, l’analyse génère des fichiers contenant différentes informations statistiques relatif à la MCMC ainsi que sur l’arbre consensus inféré.
Par défaut MrBayes exécutes deux MCMC en parralèle avec 10000 générations chacune et calcul à partir de celles-ci un score de convergence (« Average standard deviation of split frequencies ») . Un score inférieur à 0.1 signifie une convergence des chaînes.
L’inférence que nous avons exécuté a généré l’arbre consensus présenté sous format Newick à l’intérieur du fichier ArbreMB.txt Les chaînes ne semblent pas avoir convergées puisque nous avons obtenu un score de 0.19. Nous avons tout de même comparé cet
arbre à celui généré par les auteurs du programme Phylobayes à l’aide de l’applet java mentionné ci-haut et avons obtenu le résultat présenté à la figure 15. 82.1% de similarité sont partagé. On peut remarquer que les différences majeures se situent
surtout au niveau du positionnement de Encephalitis et de Dicyostelid. Nous ne pouvons conclure ici et en déduire quel arbre représente le mieux la phylogénie des séquences fournies en entrée mais il serait éventuellement possible de le faire en calculant
par exemple le facteur de Bayes.
.jpg)
Figure 15 : Comparaison d'inférence phylogénétique entre Phylobayes et MrBayes:
Phylobayes (1): maxdiff < 0.1
8. Conclusion
Ce travail à présenté un résumé des travaux effectués par l’équipe du Dr Nicolas Lartillot.
Il nous a guidé au travers les différentes méthodes d’inférence phylogénétique et les différents modèles d’évolution utilisés. Il est intéressant de noter
à quel point en phylogénie moléculaire il est nécessaire d’avoir sous la main un modèle représentant le mieux possible les mécanismes d’évolution des séquences
proteiques et d’adn pour inférer avec le maximum de probabilité l’arbre associé aux données fournit. Lartillot et al. suggère un modèle réfétant une évolution
hétérogène à la fois à travers les sites de l’alignement (CAT) et à travers le temps (BP). A première vue, ce modèle semble logique puisque la littérature
scientifique suggère fortement que que les régions fontionnelles des séquences biologiques ont tendance à être conservées au cours de l’évolution dû à la pression
sélective. De plus, les résultats de Lartillot et al. démontrent clairement l’efficacité de leur modèles par rapport à d’autres tels WAG, JTT et GTR. Néanmoins,
il est suggéré en inférence phylogénétique de tester différentes méthodes, modèles et programmes. Ensuite de choisir la combinaison qui semblerait donner
les résultats les plus fiables. Et à partir de l’arbre consensus obtenu, estimer la robustesse de la phylogénie par ‘Bootstaping’ et calculer différents
scores de qualité tel le facteur de bayes. Mais encore là, rien ne peu nous assurer que l’arbre obtenu est l’arbre réel à 100%. A tout résultat est associé
une probabilité.
Références
- Lopez,P., Casane,D., Philippe, H. Bio-informatique: Phylogénie et évolution moléculaires M/S : médecine sciences Volume 18, numéro 11, 1146-1154 (2002)
- Galtier, N. & Lobry, J. R. Relationships between genomic G1C content, RNA secondary structures, and optimal growth temperature in prokaryotes J. Mol. Evol. 44, 632– 636 (1997)
- Lartillot,N., Brinkmann, H., Philippe, H. Suppression of long-branch attraction artefacts in the animal phylogeny using a site-heterogeneous model BMC Evol Biol. 2007; 7(Suppl 1): S4.
Published online February 8. doi: 10.1186/1471-2148-7-S1-S4 (2007)
- Lartillot, N., Philippe, H. CAT : Un modèle phylogénétique Bayésien permettant de prendre en compte l’hétérogénéité des processus de substitution entre sites dans les alignments proteiques Biosystema 22, 97 -104 (2004)
- Lartillot, N., Bousseau, B., Blanquart, S., Necsulea, A. Parallel adaptations to high temperatures in the archaean eon Nature 456, 18-25 (2008)
- Lartillot, N., Blanquart, S., A. A Site- and Time-Heterogeneous Model of Amino Acid Replacement Molecular Biology and Evolution 25(5), 842-858 (2008)
- Galtier, N. & Lobry, J. R. Relationships between genomic G1C content, RNA secondary structures, and optimal growth temperature in prokaryotes. J. Mol. Evol. 44, 632–636 (1997).
- Zeldovich, K. B., Berezovsky, I. N. & Shakhnovich, E. I. Protein and DNA sequence determinants of thermophilic adaptation. PLoS Comput. Biol. 3, 62–72 (2007)
- Galtier, N., Tourasse, N.&Gouy, M.Anonhyperthermophilic common ancestor to extant life forms. Science 283, 220–221 (1999)
- Di Giulio, M. The universal ancestor and the ancestor of bacteria were hyperthermophiles. J. Mol. Evol. 57, 721–730 (2003)
- Gaucher, E. A., Thomson, J. M., Burgan, M. F. & Benner, S. A. Inferring the palaeoenvironment of ancient bacteria on the basis of resurrected proteins. Nature 425, 285–288 (2003).
- Gribaldo, S. & Brochier-Armanet, C. The origin and evolution of archaea: a state of the art. Phil. Trans. R. Soc. Lond. B 361, 1007–1022 (2006).
- Gaucher, E. A. Govindara jan, S. & Ganesh, O. K. Palaeotemperature trend for precambrian life inferred from resurrected proteins. Nature 451, 704–707 (2008).
- Fournier, G. P. & Gogarten, J. P. Signature of a primitive genetic code in ancient protein lineages. J. Mol. Evol. 65, 425–436 (2007).
- Nisbet, E. G. & Sleep, N. H. The habitat and nature of early life. Nature 409, 1083–1091 (2001).
- Sleep, N. H., Zahnle, K. J., Kasting, J. F. & Morowitz, H. J. Annihilation of ecosystems by large asteroid impacts on the early Earth. Nature 342, 139–142 (1989).
- Gogarten-Boekels, M., Hilario, E. & Gogarten, J. P. The effects of heavy meteorite bombardment on the early evolution–the emergence of the three domains of life. Orig. Life Evol. Biosph. 25, 251–264 (1995).
- Mushegian, A. R. & Koonin, E. V. A minimal gene set for cellular life derived by comparison of complete bacterial genomes. Proc. Natl Acad. Sci. USA 93, 10268–10273 (1996).
- Forterre, P. The origin of DNA genomes and DNA replication proteins. Curr. Opin. Microbiol. 5, 525–532 (2002).
- Blanquart S, Lartillot N. A Bayesian compound stochastic process for modeling non-stationary and nonhomogeneous sequence evolution. Mol Biol Evol (2006) 23:2058–2071
- Lanave C, Preparata G, Saccone C, Serio G. A new method for calculating evolutionary substitution rates. J Mol Evol 20, 86–93 (1984)
- Lartillot, N., Philippe, H. A Bayesian mixture model for across-site Heterogeneities in the Amino-Acid Replacement Process Molecular Biology and Evolution 21 no. 6, 1095–1109
(2004)
- Cavalli-Sforza, L. L. et Edwards A. W. F. Phylogenetic analysis: models and estimation procedures. American Journal of Human Genetics 19 233-257 (1967)
- Fitch, W. M. et Margoliash, E. Construction of phylogenetic trees. Science 155 279-284 (1967)
- De Soete, G. A least squares algorithm for fitting additive trees to proximity data. Psychometrika 48 621–626 (1983)
- Carraux, G., Gascuel, O. et Andrieu, G. Approches informatiques de la reconstruction d'arbres
phylogénétiques à partir de données moléculaires. TSI 14 (2) , 113-139 (1995)
- Desper, R. et Gascuel, O. Fast and Accurate Phylogeny Reconstruction Algorithms Based on the Minimum-Evolution Principle. Journal of Computational Biology 19 (5) 687-705 (2002)
- Felsenstein, J. inferring phylogenies. Sunderland (MA): Sinauer Associates 664p (2004)
- Saitou, N. et Nei, M. The neighbor-joining method: A new method for reconstructing phylogenetic trees. Molecular Biology and Evolution 4 406-425 (1987)
- Darlu, P. & Tassy, P. Reconstruction phylogénétique: concepts et méthodes. Collection Biologie Théorique, Masson, Paris 245 p (1993)
- Swofford, D. L., Olsen, G. J., Waddell, P. J. et Hillis, D. M. Phylogenetic inference. in D. M. Hillis, C. Moritz, and B. Mable (eds.) Molecular Systematics (2nd ed.), Sinauer Associates, Sunderland, Massachusetts. 407-514 (1996)
- Hendy, M. D. et Penny, D. Branch and bound algorithms to determine minimal evolutionary trees. Mathematical Biosciences 59 277-290 (1982)
- Neyman, J. Molecular studies of evolution: a source of novel statistical problems. In Gupta, S. and Yackel, J. (Eds.). Statistical Decision Theory and Related Topics NY Academic Press 1–27 (1971)
- Delsuc, F., Douzery, E.J. Les méthodes probabilistes en phylogénie moléculaire, (2) L’approche bayésienne. Biosystema 22 , Avenir et pertinence des méthodes d’analyse en phylogénie moléculaire, 75-86 (2004)
- Fitch W. M. (1966) An improved method of testing for evolutionary homology. J. Mol. Biol.,16, 9-16 (1992)
- Dayhoff M. O., Schwartz R. M. and Orcutt B. C. A model of evolutionary change in proteins. Atlas of Protein Structure, 5, Suppl. 3, 345-352 (1978)
- George D. G., Barker W.C., and Hunt L.T. . Mutation data matrix and its uses. Methods Enzymol., 183, 333-351 (1990)
- Jones D. T., Taylor W. R. and Thornton J. M. . The rapid generation of mutation data matrices from protein sequences. Comput. Appl. Biosci., 8, 275-282 (1992)
- Henikoff S. and Henikoff J. G. . Amino acid substitution matrices from protein blocks. Proc. Natl. Acad. Sci. USA, 89, 10915-10919 (1992)
- Levitt M. . A simplified representation of protein conformations for rapid simulation of protein folding. J. Mol. Biol., 104, 59-107 (1976)
- Levin J. M., Robson B. and Garnier J. An algorithm for secondary structure determination in proteins based on sequence similarity. FEBS Letters,205, 303-308 (1986)
- Risler J. L., Delorme M. O., Delacroix H. and Henaut A. Amino acid substitutions in structurally related proteins. A pattern recognition approach. J. Mol. Biol., 204, 1019-1029 (1988)
- Johnson M. S. and Overington J. P. A structural basis for sequence comparisons. An evaluation of scoring methodologies. J. Mol. Biol., 233, 716-738 (1993)
- Whelan, S., Goldman, N . A General Empirical Model of Protein Evolution Derived from Multiple Protein Families Using a Maximum-Likelihood Approach. Mol. Biol. Evol. 18(5):691–699 (2001)
- Zvelebil, M., Baum, JO. Understanding Bioinformatics. Garland Science. Chapter 8, 269-70 (2008)
- NYE, T. M., P. LIO and W. R. GILKS, A novel algorithm and web-based tool for comparing two alternative phylogenetic trees. Bioinformatics 22: 117–119 (2006)
Document préparé par Eric Fournier et Alexandre Iannello associé à la présentation
de Nicolas Lartillot dans le cadre du cours BIF7002 (HIV_09) à l'UQAM

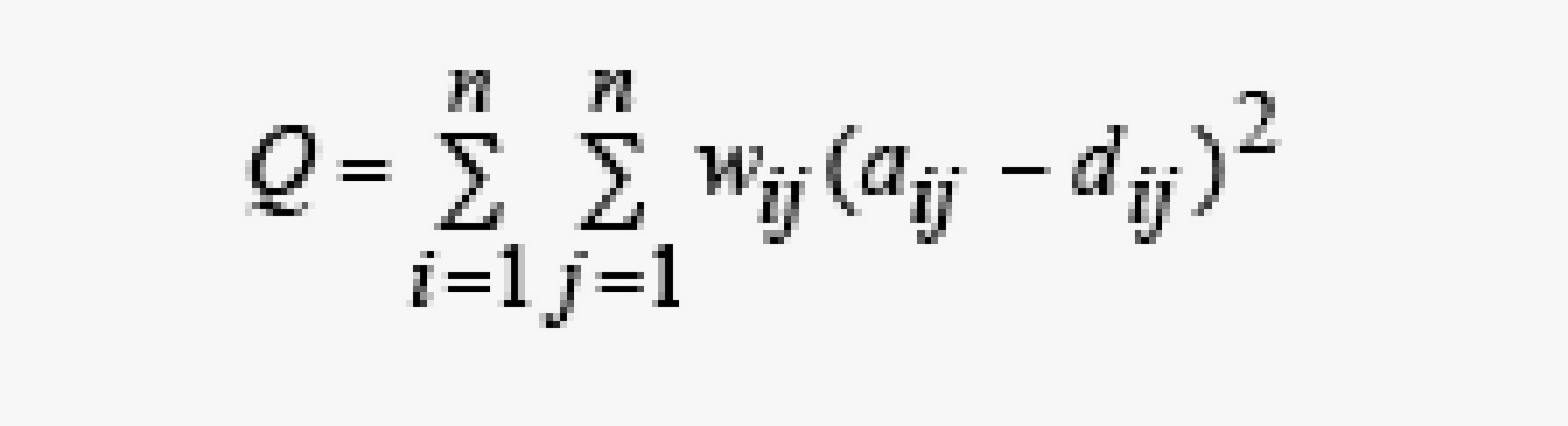

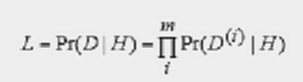
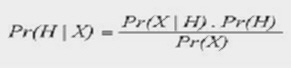
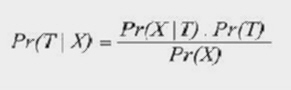











_PB(1).jpg)
.jpg)