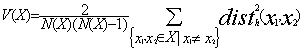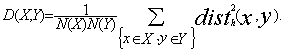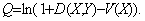conférence de Dunarel Badescu

2.3. Basée sur le potentiel oncogène

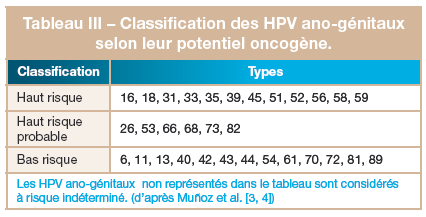
L’ancienne classification des HPVs se base sur le potentiel oncogène, on distingue les HPVs à haut risque et les HPVs à faible risque (tableau III).
Il est à noter que cette répartition ne prend en considération que les HPVs à tropisme muqueux ; cette classification étant basée sur le risque de cancer du col de l’utérus associé aux HPVs.
Les types 16 et 18 sont les plus oncogènes, les types 31, 33, 35, 51 et 52 sont considérés comme ayant un risque intermédiaire, mais sont souvent associés aux dysplasies de haut grade.
Les types 6, 11, 42, 43 et 44, considérés comme à bas risque, sont impliqués dans le développement de lésions correspondant à des condylomes acuminés qui peuvent régresser [20].

3. Épidémiologie

Les HPVs sont responsables de lésions cutanées ou muqueuses (la peau, la muqueuse de la bouche, la langue, la gorge, les amygdales, le vagin, le pénis, le col de l’utérus et l’anus), bénignes ou malignes. À ce titre les HPVs du genre alpha dits à bas risque sont à l’origine des condylomes externes génitaux, et les HPVs à haut risque sont responsables des lésions précancéreuses et cancéreuses du col de l’utérus [18].
Ils sont transmis par relations sexuelles mais aussi par contact peau à peau.
L’incidence de l’infection dans la population générale varie de 8 à 20%. Elle est plus élevée pour le Québec.
En ce qui concerne le cas spécifique du cancer du col de l’utérus, on dénombre un demi million de nouveau cas chaque année [1, 3, 15].

4. Phylogénie du génome entier des HPVs

Lors des travaux de Dunarel et al, 83 génomes de HPVs étaient entièrement séquencés et disponibles dans la base de donnés de l’ICTV. Les séquences de ces génomes ont été alignées via ClustalW, produisant ainsi un alignement de 10426 colonnes.
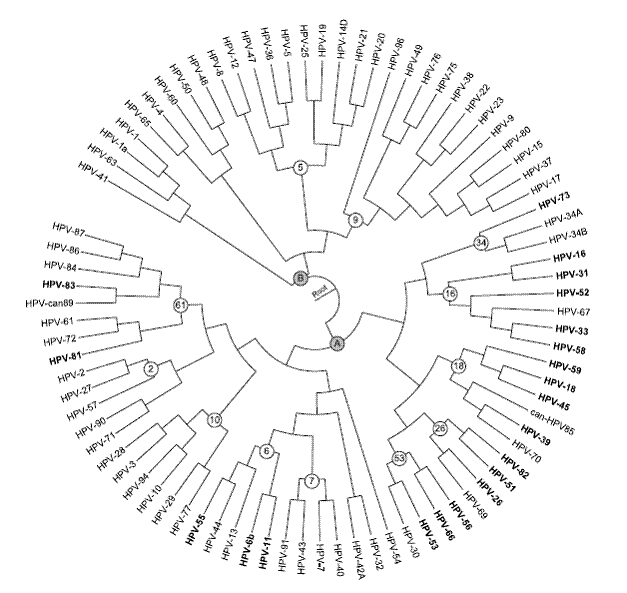
L’arbre phylogénétique de ces 83 HPVs (figure 2) a été inféré grâce au programme PHYML program [12] avec le modèle de substitution HKY. Les scores de bootstrap étaient calculés dans le but de déterminer la robustesse des branches en utilisant 100 réplicats. La plupart des branches ont un score de plus de 80%, mais dans un souci de lisibilité les auteurs n’ont pas représenté les bootstraps sur la figure 2. Le virus du papillome du bovin a servi d’outgroup afin d’enraciner l’arbre.
Cet arbre est le premier arbre phylogénétique des HPVs inféré à partir des génomes entiers (de l’affirmation des auteurs et après vérification de notre part).
L’analyse révèle la présence de 14 groupes monophylétiques dont 12 connus qui sont indiqués par des numéros sur la figure 2. Les numéros correspondent à ceux du NCBI (taxonomy browser HPV).
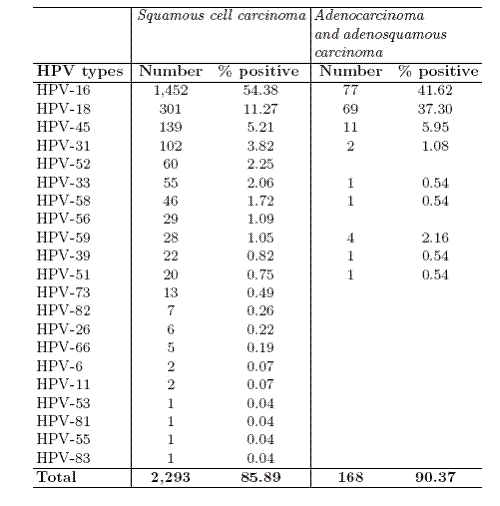
Pour définir les types carcinogènes les auteurs se sont appuyés sur une étude épidémiologique portant sur 3607 femmes de 25 pays [16, 17]. Cette étude présente les différents types de HVPs considérés comme carcinogènes comme le montre le tableau IV adapté de l’article [16]. Ces génotypes carcinogènes sont présentés en gras sur l’arbre.

Tableau IV : distribution des HPVs pour les types de cancer adineux et squameux [16]

Cet arbre est cohérent par rapport à celui de l’ICTV [13] qui a été construit à partir des séquences du gène L1.
La plupart des HPVs dangereux se retrouvent dans les sous-arbres enracinés par les nœuds 16 et 18.

Cependant cette étude ne prend en compte que les HPVs impliqués dans le cancer du col de l’utérus, or il a été démontré que les HPVs peuvent être impliqués dans d’autres cancers tel que le cancer de la peau associé à la maladie héréditaire Epidermodysplasia verruciformis[14]. Il pourrait y avoir donc d’autres génotypes cancéreux non mentionnés dans l’arbre.

Figure 2 : arbre phylogénétique de 83 génotypes de HPVs obtenu avec PHYML

Ø Arbre obtenu avec PAUP

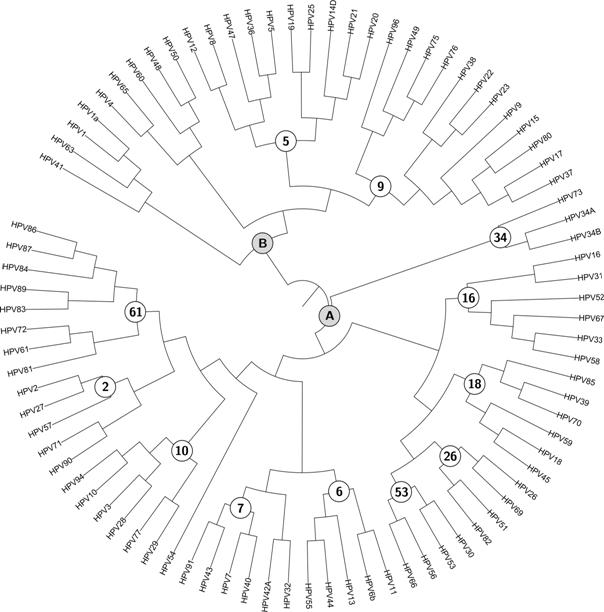
À partir des données utilisées par Dunarel et al, on a construit un arbre phylogénétique à l’aide d’une autre méthode : on a utilisé PAUP avec le maximum de vraisemblance. On a obtenu l’arbre de la figure 3.
On note trois petites différences avec l’arbre de Dunarel et al. Tout d’abord, le nœud 34 est un descendant direct du nœud A dans notre arbre alors qu’il y a deux ancêtres entre le nœud 34 et le nœud A dans celui de Dunarel et al. De plus, dans l’arbre de la figure 2, les nœuds 7 et 6 descendent du même ancêtre alors que dans le notre, il y a d’abord un ancêtre commun au nœud 7 et à l’ancêtre de HPV 42A et HPV 32. La dernière différence se situe au niveau de HPV 54 : dans notre arbre son premier ancêtre est également l’ancêtre des nœuds 2, 10, 61 et de l’ancêtre commun de HPV 61, HPV 72 et HPV 81 alors que dans l’arbre de Dunarel et al, il n’est l’ancêtre que des nœuds 6, 7 et de l’ancêtre commun de HPV 42A et HPV 32. En revanche, le sous-arbre enraciné en B est totalement identique et ne contient que des espèces non carcinogènes. Donc d’un point de vue de la carcinogènicité les deux arbres sont identiques.

Figure 3 : arbre phylogénétique des HPVs obtenu avec le logiciel PAUP

5. Phylogénie des HPVs et distribution des indels

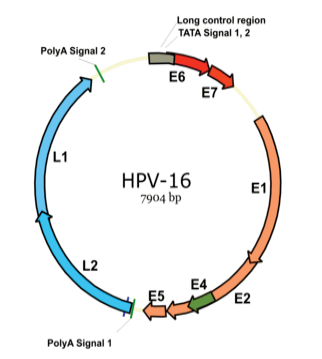
Les phénomènes d’insertion et de délétion (indels) peuvent jouer un rôle dans le caractère carcinogène des virus. 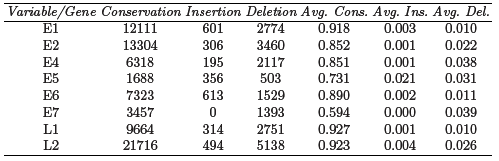Pour vérifier cette hypothèse, on peut calculer le scénario d’indel le plus probable étant donné l’arbre phylogénétique obtenu précédemment et l’alignement de chacun des principaux gènes E1, E2, E4, E5, E6, E7, L1 et L2 selon les méthodes heuristiques développées dans les articles référencés [9] et [10]. Le tableau V montre le nombre de conservations, de délétions et d’insertions dans le scénario obtenu pour chacun des gènes.

Tableau V : le nombre et la moyenne des conservations, insertions et délétions durant l’évolution pour chacun des 8 principaux gènes des HPVs [9].

Les gènes E1, L1 et L2 montrent plus de 90% de conservation, les gènes E2, E4 et E6 entre 80% et 90%, le gène E5 73% et le gène E7 59%. De plus, le taux le plus élevé d’indels a été constaté dans le sous arbre enraciné au nœud 61 où le risque carcinogène est assez bas. Plus généralement, les branches du sous-arbre enraciné au nœud A (où se trouvent tous les types carcinogènes) connaissent un taux d’indel assez bas. On peut en déduire que les virus carcinogènes ont hérité leur caractère carcinogène de leur plus proche ancêtre commun.

6. Les histoires d’évolution des différents gènes

Dans l’optique de déterminer si tous les gènes ont la même histoire évolutive ou non, l’arbre phylogénétique de chacun des principaux gènes, E1, E2, E4, E5, E6, E7, L1 et L2, a été construit avec la même méthode que celle utilisée pour les génomes complets, mais seulement pour 70 virus (à cause du manque d'informations sur les séquences de certains gènes pour les 13 autres virus). Pour chacun de ces gènes, ils ont alors mesuré la distance topologique de Robinson et Foulds (se référer au chapitre 7) entre l'arbre du gène et les arbres des 7 autres gènes. 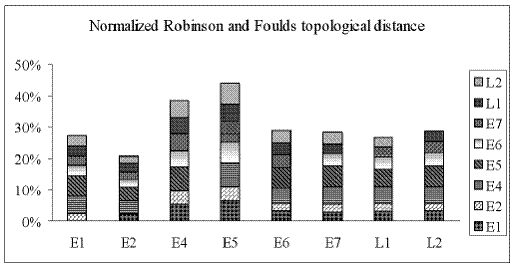Ces distances ont été normalisées par rapport à la distance maximale entre deux arbres binaires (2n-6) et exprimées en pourcentage. La figure 4 représente les résultats ainsi obtenus.
On remarque que ce sont les phylogénies des gènes E4 et E5 qui diffèrent le plus, en moyenne, des autres phylogénies : environ 5,5% en moyenne pour E4, et environ 6% pour E5, alors que c’est la phylogénie du gène E2 qui diffère le moins en moyenne des autres phylogénies : environ 3% en moyenne. Ces différences ne sont pas assez significatives pour conclure que la différenciation d’un gène particulier est responsable de l’acquisition de la carcinogénicité. En revanche, ces différences confirment l’hypothèse de l’importance des phénomènes de recombinaison chez les HPVs. Par exemple, une étude approfondie de Angulo et Carjaval-Rodriguez [1] démontre que le gène L2 a subi des recombinaisons chez presque tous les génotypes tandis que les gènes L1 et E6 sont ceux qui ont la plus grande fréquence de recombinaisons. Le gène E7 quant à lui ne semble avoir subi des recombinaisons que dans le type HPV 16.

7. Distance de Robinson et Foulds.

On reprend ici l’exposition originale de Robinson et Foulds [19]. On se référera à cet article pour les démonstrations des résultats énoncés ci-dessous. On veut définir une distance topologique entre les arbres phylogénétiques. On ne tient pas compte de la longueur des branches mais seulement de la topologie des arbres.
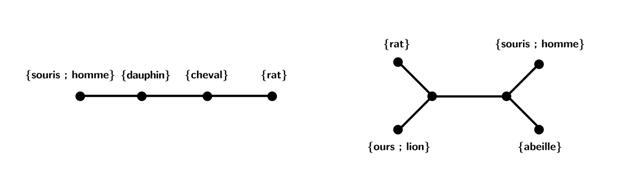
Soit S un ensemble de n espèces (n>1). Un arbre phylogénétique T* sur S est la donnée d’un arbre T à m sommets P = {p1, p2, ¼, pm}, et d’une partition de S en m sous-ensembles S1, S2, ¼, Sm tels que Si peut être vide si et seulement si pi est de degré strictement plus grand que 2. On confondra par la suite les notations T* et T. Un arbre phylogénétique « classique » correspond au cas d’un arbre binaire où à chaque feuille pi correspond une espèce et où Si est vide si pi n’est pas une feuille. On donne deux exemples ci-dessous.

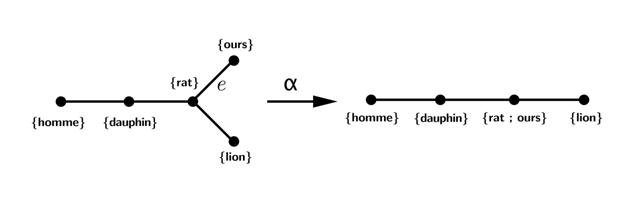
On définit alors deux opérations sur les arbres phylogénétiques. La première s’appelle contraction et est notée a. Elle consiste en la fusion de deux sommets pr et pq en un seul sommet. Le sous-ensemble de S correspondant à ce nouveau sommet est alors l’union de Sr et Sq. On donne deux exemples ci-dessous où on contracte l’arête e.

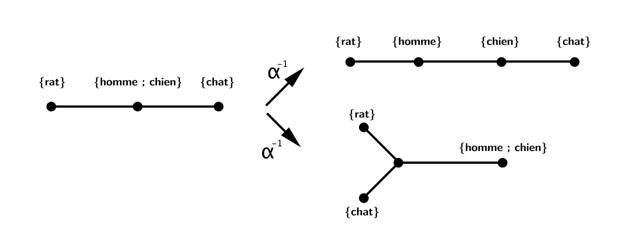
On définit une deuxième opération notée a-1 et appelée expansion. Elle consiste en la séparation d’un sommet pr en deux sommets distincts reliés par une arête. On répartit alors Sr et les arêtes de pr entre les deux nouveaux sommets. Il y a plusieurs choix possibles. On donne deux exemples ci-dessous pour le même sommet.

Si on note US l’unique arbre phylogénétique à un sommet, on voit facilement qu’on peut transformer un arbre T à m sommets en l’arbre US à l’aide de m-1 opérations de contraction. Chacune de ces opérations étant inversible par une opération a-1, on peut passer de US à T à l’aide de m-1 opérations d’expansion. On peut ainsi passer d’un arbre T1 à un arbre T2 en au plus n+m-2 opérations de contraction et d’expansion.

Définition : Soient T1 et T2 deux arbres phylogénétiques. La distance de Robinson et Foulds entre ces deux arbres, notée d(T1,T2) est égale au nombre minimum de transformations a et a-1 nécessaires pour passer de T1 à T2.
On peut bien parler de distance puisqu’on peut vérifier facilement les propriétés suivantes pour tous les arbres T1,T2 et T3 :
·    d(T1,T2)>0
·    d(T1,T2)=0 si et seulement si T1=T2
·    d(T1,T2)= d(T2,T1)
·    d(T1,T2)< d(T1,T3) +d(T3,T2)
On peut montrer que la distance maximale entre deux arbres à n espèces est égale à 3n-6, et 2n-6 pour les arbres binaires avec une espèce sur chaque feuille.

On peut calculer cette distance à l’aide de fonctions de partition. On note E l’ensemble des arêtes d’un arbre T. Toute arête e de T partitionne S en deux ensembles disjoints. On note f(e) cette partition. Soient T1 et T2 deux arbres phylogénétiques, on note f1 et f2 leurs fonctions de partition, E1 et E2 leurs ensembles d’arêtes. On définit alors les deux ensembles suivants :
F1={e1 £ E1, $ e2 £ E2, tel que f1(e1)=f2(e2)}
F2={e2 £ E2, $ e1 £ E1, tel que f2(e2)=f1(e1)}
On peut alors montrer que la distance de Robinson et Foulds se calcule par la formule suivante :

d(T1,T2)=card(E1\F1)+ card(E2\F2),

où E1\F1 désigne le complémentaire de F1 dans E1, et card désigne le cardinal, i.e., le nombre d’éléments, d’un ensemble fini.

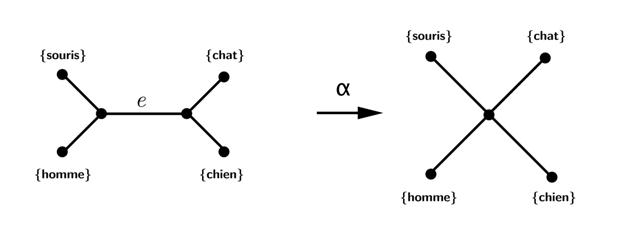
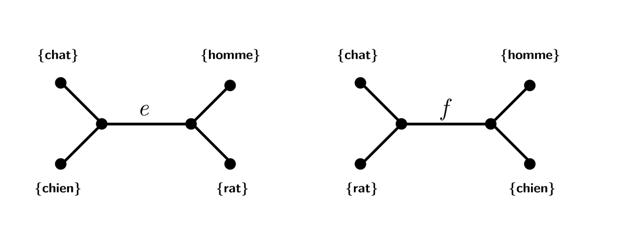
On donne un exemple de calcul ci dessous. On veut calculer la distance entre les deux arbres suivants :

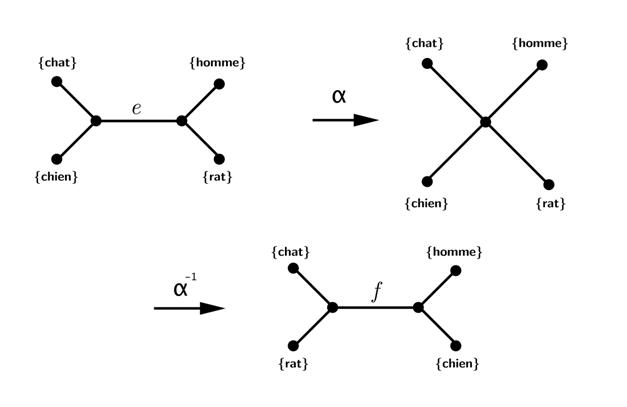
En utilisant la définition, on obtient une distance de 2 car on peut passer du premier arbre au deuxième par les deux transformations suivantes :

On peut aussi calculer cette distance à l’aide des fonctions de partitions. On a en effet E1\F1={e} et E2\F2={f}. On obtient alors une distance de 1+1=2.

8. Identification de régions potentiellement carcinogènes

Cette étape a pour but la détermination de régions génomiques susceptibles d'être responsables de la nature carcinogène des VPHs. On cherche ainsi des régions qui sont fortement similaires chez les virus carcinogènes et qui présentent des différences importantes entre les virus carcinogènes et les virus non carcinogènes. Pour ce faire, les virus ont été regroupés dans deux classes : carcinogène noté X, et non carcinogène noté Y. Les études ont été menées gène par gène. Pour chaque alignement de gènes, et pour chaque paire de virus, on a calculé la distance de Hamming normalisée entre toutes les sous-séquences de taille k, k allant de 3 à 20. La distance de Hamming normalisée entre deux séquences alignées x1 et x2, notée disth(x1,x2), est le nombre total de mismatchs dans l’alignement divisé par la longueur de la séquence. Pour tout entier k entre 3 et 20, et pour chaque position i de l’alignement, on calcule les nombres suivants :

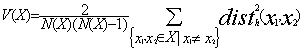
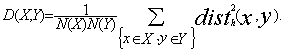
où chaque somme porte sur toutes les séquences de taille k commençant en position i, et où N(X) (respectivement N(Y)) est le nombre de virus de type X (respectivement de type Y). On dit qu’on a scanné la fenêtre de largeur k commençant en position i. Puis on calcule la fonction

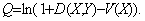
Cette fonction est majorée par ln(2). Plus cette fonction est grande, plus la séquence identifiée est différente entre les virus carcinogènes et non carcinogènes, et plus la séquence est conservée chez les virus carcinogènes. On utilise la distance de Hamming car on considère des petites séquences et on veut considérer les gaps comme des caractères à part entière. On fait le même calcul pour les fenêtres non chevauchantes de taille 20. L’algorithme utilisé est présenté ci-dessous. Étant donnés un alignement multiple correspondant à deux groupes de virus X et Y, des tailles de fenêtres allant de WIN_MIN à WIN_MAX, et un seuil TH, l’algorithme trouve toutes les régions (position sur l’alignement, taille de la fenêtre et valeur de Q) qui donnent une valeur de Q supérieure au seuil. On prend S=1 si on veut considérer toutes les fenêtres et S égal à la taille des fenêtres si on ne veut que les fenêtres non chevauchantes. La vitesse de cet algorithme est de l’ordre de l*w*n2 pour chaque taille de fenêtre w, où l est la longueur de l’alignement et n le nombre d’espèces. On peut réduire la complexité à l*n2 si on évite de recalculer des distances déjà calculées quand on décale la fenêtre d’une position.

Algorithm 1. Algorithmic scheme (MSA, MSA_L,X, N(X), Y, N(Y), WIN_MIN,
WIN_MAX, S, TH)

Require: MSA:            Multiple sequence alignment (considered as a matrix),
               MSA_L:             Length of MSA,
               X:                 Set of carcinogenic taxa,
               N(X):             Cardinality of the set X,
               Y:                 Set of non-carcinogenic taxa,
               N(Y):             Cardinality of the set Y,
               WIN_MIN:         Minimum sliding window width,
               WIN_MAX:        Maximum sliding window width,
               S:                 Sliding window step,
               TH:             Minimum Q value for Hit (i.e., hit threshold).

Ensure:   Set of Hit Regions:     (win_width, idx, Q), where
    Win_width:         Current sliding window width,
               idx:             Hit Index (i.e., its genomic position),
               Q:                 Value of the hit region identification function.

1: for win width from WIN_MIN to WIN_MAX do
2:     for idx from 0 to MSA_L−win width with step S do
3:         MSA_X ← MSA[X][idx..idx + win_width]
4:         MSA_Y ← MSA[Y ][idx..idx + win_width]
5:         V (X) ← D(X, Y ) ← 0
6:         for all distinct i, j Î X do
7:             V (X) ← V (X) + disth2(MSA_X[i], MSA_X[j])
8:         end for
9:         V (X) ← 2 × V (X)/(N(X) × (N(X) − 1))
10:         for each i Î X and j Î Y do
11:             D(X, Y ) ← D(X, Y ) + dis th2 (MSA_X[i], MSA_Y[j])
12:         end for
13:         D(X, Y ) ← D(X, Y )/(N(X) × N(Y ))
14:         Q ← ln(1 + D(X, Y ) − V (X))
15:         if Q > TH then
16:             identify the current region (win width, idx, Q) as a hit region
17:         end if
18:     end for
19: end for

Les résultats sont présentés dans le tableau VI dans le cas de fenêtres chevauchantes de tailles 13 à 20. Les calculs ont été effectués gène par gène. Plus de 35 000 résultats donnaient des valeurs de Q supérieures à 0,25. Les résultats présentés dans ce tableau ont été sélectionnés manuellement parmi les 100 meilleurs scores en sélectionnant les régions les plus longues possibles (quitte à obtenir des valeurs de Q moins élevées car plus la largeur de la fenêtre est petite, plus on obtient des valeurs de Q élevées). On trouve 4 scores au dessus de 0,5 : 2 pour le gène E6, 1 pour le gène E2 et 1 pour le gène L1.

Tableau VI : Sélection de régions potentiellement responsables de la carcinogénicité

Conclusion et perspectives

La valeur de Q semble être un bon indicateur de la responsabilité éventuelle d'une région génomique dans la carcinogénicité d'un HPV. En effet, la plupart des grandes valeurs de Q ont été obtenues au niveau des gènes E2 et E6 qui semblent jouer un rôle important dans les cancers cervicaux. Cependant, la plus grande valeur de Q a été observée pour une région du gène L1. Les protéines des capsides des HPVs carcinogènes pourraient ainsi avoir une région spécifique, ce qui pourrait permettre le développement d'un vaccin. De plus, la plupart des valeurs de Q élevées sont associées à des fenêtres de petite taille, ce qui semble favoriser les substitutions par rapport aux délétions.
Il serait intéressant de déterminer les scénarios évolutifs les plus probables pour chacune des régions identifiées. On pourrait ainsi déterminer quand a été introduite la carcinogénicité des HPVs.

Références

1. Angulo, M., Carvajal Rodriguez, A.: Evidence of recombination within human alpha-papillomavirus. Virology Journal 4, 33 (2007)

2. Antonsson, A., Forslund, O., Ekberg, H., Sterner, G., Hansson, B.G.: The Ubiquity and Impressive Genomic Diversity of Human Skin Papillomaviruses Suggest a Commensalic Nature of These Viruses. Journal of Virology 74(24), 11636–11641 (2000)

3. Bosch, F.X., Manos, M.M., Muoz, N., Sherman, M., Jansen, A.M., Peto, J., Schiffman, M.H., Moreno, V., Kurman, R., Shan, K.V.: Prevalence of Human Papillomavirus in Cervical Cancer: a Worldwide Perspective. International Biological Study on Cervical Cancer (IBSCC) Study Group. Journal of the National Cancer Institute 87(11), 796–802 (1995)

6. Combita, A.-L., Touz, A., Bousarghin, L., Christensen, N.D., Coursaget, P.: Identification of Two Cross-Neutralizing Linear Epitopes within the L1 Major Capsid Protein of Human Papillomaviruses. Journal of Virology 76(13), 6480–6486 (2002)

8. De Villiers, E.M., Fauquet, C., Broker, T.R., Bernard, H.U., Zur Hausen, H.: Classification of papillomaviruses. Virology 324(1), 17–27 (2004)

9. Diallo, A.B., Makarenkov, V., Blanchette, M.: Exact and Heuristic Algorithms for the Indel Maximum Likelihood Problem. Journal of Computational Biology 14(4), 446–461 (2007)

10. Diallo, A.B., Makarenkov, V., Blanchette, M.: Finding maximum likelihood indel scenarios. In: Proceeding of the fourth Recomb satellite conference on Comparative Genomics, pp. 171–185 (2006)

11. Dunarel Badescu, Abdoulaye Banire Diallo, Mathieu Blanchette, Vladimir Makarenkov. An Evolutionary Study of the Human Papillomavirus Genomes (2008)

12. Guindon, S., Gascuel, O.: A simple, fast, and accurate algorithm to estimate large phylogenies by maximum likelihood. Systematic Biology 52, 696–704 (2003)

13. Bchen-Osmond: ICTVdB - The Universal Virus Database C (ed). Columbia University, New York, USA

14. Jablonska, S; Dabrowski, J; Jakubowicz, K. Epidermodysplasia verruciformis as a model in studies on the role of papovaviruses in oncogenesis. Cancer Res. 1972;32:583–589. [PubMed]

15. Muñoz, N.: Human papillomavirus and cancer: the epidemiological evidence. Journal of Clinical Virology 19(1-2), 1–5 (2000)

16. Muñoz, N., Bosch, F.X., de Sanjos, S., Herrero, R., Castellsagu, X., Shah, K.V., Snijders, P.J.F., Meijer, C.J.L.M.: Epidemiologic classification of human papillomavirus types associated with cervical cancer. New England Journal of Medecine 384, 518–527 (2003)

17. Muñoz, N., Bosch, F.X., Castellsagu, X., Daz, M., de Sanjose, S., Hammouda, D., Shah, K.V., Meijer, C.J.: Against which human papillomavirus types shall we vaccinate and screen? The international perspective. International Journal of Cancer 111, 278–285 (2004)

18. Prétet, J.L., Charlot, J.F., Mougin, C.: Virological and carcinogenic aspects of HPV. Bulletin Academic National de Medecine 191(3), 611–613 (2007)

19. Robinson, D.R., Foulds, L.R.: Comparison of phylogenetic trees. Mathematical Biosciences 53, 131–147 (1981)

20. Segondy M, Classification des papillomavirus (HPV) Revue francophone des laboratoires, septembre-octobre 2008

21. Tortolero-Luna, G. « Epidemiology of genital HPV », Hematology and Oncology Clinics of North America, vol. 13, n° 1, février 1999, p. 245-257.